※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해 초기의 컴퓨터는
8bit 단위로 연산하고 데이터를 처리하는 것이 효율적임을 알 수 있었다.
그래서 현재까지도 데이터 연산 및 처리 단위를 1byte(8bit)로 시작하여
2byte(16bit), 4byte(32bit), 8byte(64bit) 등
2의 거듭제곱을 따른다는 것을 알게 되었다.
이에 따라
산술/논리연산 회로를 포함한 메모리 회로도 1byte(8bit) 단위로 구현해 보았다.
그러면서 실질적으로 메모리 회로가 유용하게 사용되기 위해서는
D래치와 출력제어기를 결합한 레지스터라는 장치로 사용됨을 알 수 있었다.
[컴퓨터][20] 바이트와 출력 제어기 그리고 레지스터( Byte , Enabler , Register )
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다. 이전 글들을 통해 메모리 회로가 필요하게 된 이유는산술/논리 연산 회로 중에서 나눗셈 연산 회로를 구현하기
core-basic.tistory.com
이어서 이번 글을 통해 원래 목적이었던
나눗셈 연산을 회로로 어떻게 구현할 수 있는지 탐구해 보겠다.
나눗셈 연산 회로
(산술/논리연산 회로와 레지스터)
< 나눗셈 연산 과정>
나눗셈 연산과정에 대한 자세한 내용은 다음 글을 통해 파악할 수 있다.
[컴퓨터][17] 산술/논리 연산 회로 - 5 (나눗셈 회로와 비교 연산 그리고 메모리)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서컴퓨터는 초기에 산술/논리 연산 등 수학적 계산을 자동화하고자설계되었다는 것을 알게 되었
core-basic.tistory.com
요약하면 A ÷ B (A > B)에 대해서
- 1 -
큰 값(A)을 나머지로 취급하여, 각 자릿값과 나누는 값(B)을 비교한다.
- 2 -
A의 각 자리마다 B를 뺄 수 있는 만큼 반복해서 빼고,
그 뺀 횟수가 해당 자리의 몫이 된다.
- 3 -
A의 마지막 자리에서 더 이상 뺄 수 없을 때 남은 값이 최종 나머지가 된다.
그리고 이를 회로적 측면에서 보면 다음과 같다.
A ÷ B (A > B)에 대해서
- 1 -
A의 가장 왼쪽 자리 값을 나머지 레지스터의 첫 번째 비트에 입력한다.
- 2 -
나머지와 나누는 값(B)을 비교하여 빼지 못한다면(나누지 못한다면)
가장 왼쪽 자리의 몫은 0으로 처리한다.
또는 나머지와 나누는 값(B)을 비교하여 뺄 수 있다면(나눌 수 있다면)
가장 왼쪽 자리의 몫은 1로 처리한 후, 나머지에서, 나누는 값(B)을 뺀다.
- 3 -
이후 나머지에 대해서 왼쪽 시프트 연산을 진행한다.
- 4 -
이후 A의 가장 왼쪽 자리의 다음 자리인 값을
또 나머지의 첫 번째 비트로 보내어,
더 이상 나머지로 보낼 비트가 없을 때까지 반복한다.
따라서 나눗셈 연산을 하는데 다음과 같은 회로만 준비되어 있다면
나눗셈 연산을 진행할 수 있다.
(1) 레지스터
(2) 비교기
(3) 덧셈/뺄셈 연산기
(4) 왼쪽 시프트 연산기
위의 준비물은 모두 이전 글들을 통해 구현하였으므로 나눗셈 연산이 가능하다.
[컴퓨터][20] 바이트와 출력 제어기 그리고 레지스터( Byte , Enabler , Register )
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다. 이전 글들을 통해 메모리 회로가 필요하게 된 이유는산술/논리 연산 회로 중에서 나눗셈 연산 회로를 구현하기
core-basic.tistory.com
하지만 실질적으로 회로를 통해 나눗셈 연산을 진행하는 과정은
산술/논리 연산을 통해
최상위 비트부터 자리값을 구하는 과정과,
최하위 비트의 값만 변경하는 과정이
추가되는 등 좀 더 복잡하다.
따라서
이에 대해 음수와 소수를 제외하고, 자연수만 다루는 8bit 나눗셈 연산 회로를
예시로 하여 실질적으로 어떻게 회로로 나눗셈 연산이 진행되는지 알아보겠다.
<회로에 대입한 나눗셈 연산>
ex) 1000 0110(86) ÷ 0000 0010(2) = 0100 0011(43) + 0
[0]
초기화 (초기값 설정)
A(나눠질 값) 레지스터 : 1000 0110
B(나누는 값) 레지스터 : 0000 0010
C(나머지) 레지스터 : 0000 0000
D(몫) 레지스터 : 0000 0000
< A(나눠질 값) 레지스터 : D = 1000 0110, S = 1, E = 0 >

< B(나누는 값) 레지스터 : D = 0000 0010, S = 1, E = 0 >

< C(나머지) 레지스터 : D = 0000 0000, S = 1, E = 0 >

< D(몫) 레지스터 : D = 0000 0000, S = 1, E = 0 >

[1]
A(1000 0110)의 가장 왼쪽 자리 값만(1) 따로 구하기 위해서,
A(나눠질 값)레지스터 값을 출력하여 왼쪽 시프트 연산을 진행한다.
이때 연산 결과에서 발생한 자리올림 비트 값이 해당 자리값이 되며,
연산 결과는 다시 A레지스터에 저장한다.
< A 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 1000 0110 >

< 왼쪽 시프트 연산 : SHL 1000 0110 (CI = 0) ⇒ 0000 1100 (CO = 1)>

< A 레지스터 저장 : D = 0000 1100, S = 1, E = 0>

[2]
왼쪽 시프트 연산 결과로 발생한 자리올림 비트 값(A의 가장 왼쪽 자리 값)과
C(나머지) 레지스터 값을 확인하여 두 값을 덧셈기를 통해 더한다.
그리고
그 결과를 C(나머지) 레지스터에 입력함으로써
A의 가장 왼쪽 자리 값을 C(나머지) 레지스터의 첫 번째 비트에 입력한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0000>

< 덧셈기 : 1 + 0000 0000 = 0000 0001 >

< C 레지스터 입력 : D = 0000 0001, S = 1, E = 0>

[3]
C(나머지) 레지스터에서 E = 1으로 변경하여 저장된 값을 확인하여,
B(나누는 값)과 함께 비교기에 입력하여 비교한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0001 >

< B 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0010 >

< 비교기 : CMP (0000 0001, 0000 0010) ⇒ A > B = 거짓(0), A = B = 거짓(0) >

이때 연산 결과에서 발생한 (A > B의 비트 값 OR A = B의 비트값)이
D 레지스터(몫)의 가장 왼쪽 자리 값이 된다.
이에 대해 실질적으로는 각 과정마다 D레지스터의 값과 더한 후
왼쪽 시프트 연산을 해주면 최종적으로는 가장 왼쪽 자리의 값이 된다.
< D 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0000 >

< 덧셈기 : ADD (0, 0000 0000) ⇒ 0000 0000 >

< D 레지스터 입력 : D = 0000 0000, S = 1, E = 0 >

< D 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0000 >

< 왼쪽 시프트 연산 : SHL D(0000 0000) ⇒ 0000 0000 >

< D 레지스터 입력 : D = 0000 0000, S = 1, E = 0 >

[4]
그리고 앞선 [3]의 비교 연산 결과에서 A > B = 0 일경우
C(나머지) - B(나누는 값) 연산이 불가능하므로 다음 단계로 넘어간다.
만약 A > B = 1 일 경우 C(나머지)-나누는 값(B) 연산이 가능하므로
뺄셈 기를 통해 C - B를 진행하고 그 결과를 다시 C(나머지)에 저장한다.
[5]
C(나머지) 레지스터 값을 왼쪽 시프트 연산한 후
다시 C(나머지) 레지스터에 저장한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0001 >
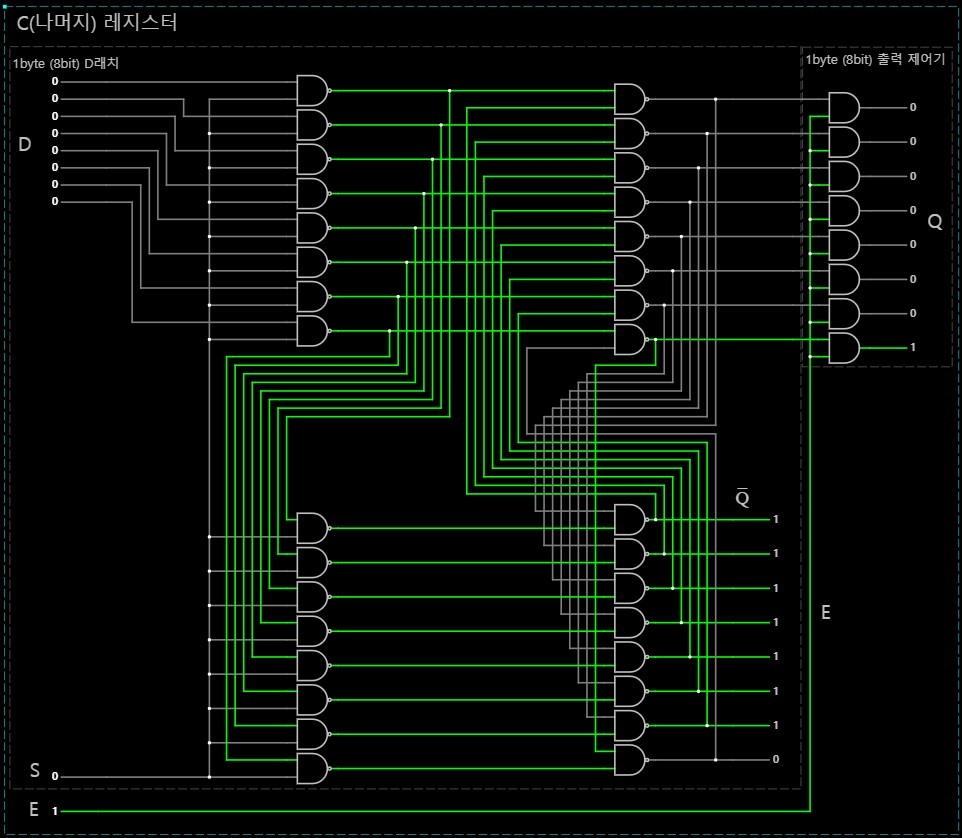
< 왼쪽 시프트 연산 : SHL 0000 0001 (CI = 0) ⇒ 0000 0010 (CO = 0)>

< C 레지스터 입력 : D = 0000 0010, S = 1, E = 0 >

이처럼 8bit 나눗셈 연산은 (1)~(5)의 과정을 8번 반복하면 된다.
그리고 그 결과로 나오는
C(나머지) 레지스터 값이 최종 나머지가 되고,
D(몫) 레지스터가 최종 몫이 된다.
이어서 그러면 앞에서 자리값이 1일 때의 경우를 살펴보았으므로,
자리값이 0이고 A > B = 1 일 경우 그리고,
C(나머지)-나누는 값(B) 연산하는 과정까지 살펴보겠다.
[6]
다시 원래 A(1000 0110)의 가장 왼쪽자리에서
다음 자리(7번째 자리) 값(0)을 따로 구하기 위해서,
이미 한 번 왼쪽 시프트 연산된 A레지스터 값(0000 1100)을 출력하여
왼쪽 시프트 연산을 진행한다.
이때 연산 결과에서 발생한 자리올림 비트 값이 해당 자리값이 되며,
연산 결과는 다음 연산을 위해 다시 A레지스터에 저장한다.
< A 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 1100 >

< 왼쪽 시프트 연산 : SHL 0000 1100 (CI = 0) ⇒ 0001 1000 (CO = 0)>

< A 레지스터 저장 : D = 0001 1000, S = 1, E = 0>

[7]
그리고 왼쪽 시프트 연산 결과로 발생한
자리올림 비트 값(A의 가장 왼쪽 자리 값)과
C(나머지) 레지스터 값을 확인하여
두 값을 덧셈기를 통해 더한다.
그리고 그 결과를 C(나머지) 레지스터에 입력함으로써
A의 가장 왼쪽 자리 값을 C(나머지) 레지스터의 첫 번째 비트에 입력한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0010>

< 덧셈기 : 0 + 0000 0010 = 0000 0010 >

< C 레지스터 입력 : D = 0000 0010, S = 1, E = 0>

[8]
C(나머지) 레지스터에서 E = 1으로 변경하여 저장된 값을 확인하여,
B(나누는 값)과 함께 비교기에 입력하여 비교한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0010 >

< B 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0010 >

< 비교기 : CMP (0000 0001, 0000 0010) ⇒ A > B = 거짓(0), A = B = 참(1) >

이때 연산 결과에서 발생한 (A > B의 비트 값 OR A = B의 비트값)이
D 레지스터(몫)의 가장 왼쪽 자리 값이 된다.
이에 대해 실질적으로는 각 과정마다 D레지스터의 값과 더한 후
왼쪽 시프트 연산을 해주면 최종적으로는 가장 왼쪽 자리의 값이 된다.
< D 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0000 >

< 덧셈기 : ADD (1, 0000 0000) ⇒ 0000 0001 >

< D 레지스터 입력 : D = 0000 0001, S = 1, E = 0 ⇒ 0000 0001 >

< D 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0001 >

< 왼쪽 시프트 연산 : SHL D(0000 0001) ⇒ 0000 0010 >

< D 레지스터 입력 : D = 0000 0001, S = 1, E = 0 ⇒ 0000 0010 >

[9]
그리고 앞, [8]에서 비교기 연산 결과가 A > B = 1 또는 A = B가 1일 경우
C(나머지)-나누는 값(B) 연산이 가능하므로 뺄셈기를 통해
C - B를 진행하고 그 결과를 다시 C(나머지)에 저장한다.
만약 앞선 비교 연산 결과에서 A > B = 0 일경우 C(나머지) - B(나누는 값)
연산이 불가능하므로 다음 단계로 넘어간다.
< C 레지스터 출력 : C = 0000 0000, S = 0, E = 1 ⇒ 0000 0010 >

< B 레지스터 출력 : B = 0000 0000, S = 0, E = 1 ⇒ 0000 0010 >

< 뺄셈기 : SUB (0000 0010, 0000 0010) = 0000 0000 >

< C 레지스터 입력 : C = 0000 0000, S = 1, E = 0 >

[10]
C(나머지) 레지스터 값을 왼쪽 시프트 연산한 후
다시 C(나머지) 레지스터에 저장한다.
< C 레지스터 출력 : D = 0000 0000, S = 0, E = 1 ⇒ 0000 0000 >

< 왼쪽 시프트 연산 : SHL 0000 0000 (CI = 0) ⇒ 0000 0000 (CO = 0) >

< C 레지스터 입력 : D = 0000 0000, S = 1, E = 0 >

따라서 지금까지
1000 0110(86) ÷ 0000 0010(2) = 0100 0011(43) + 0 연산 과정 중에서
최상위 2bit에 대한 연산을 진행하여서 다음과 같은 결과를 얻었다.
A(나눠질 값) 레지스터 : 0001 1000
B(나누는 값) 레지스터 : 0000 0010
C(나머지) 레지스터 : 0000 0000
D(몫) 레지스터 : 0000 0010
위의 과정을 통해서 나눗셈 연산을 진행할 때
각 자리값이 0 또는 1, 두 가지 상황에 대해서
어떻게 처리해야 하는 파악 하였으므로
해당 bit 수만큼 반복하다 보면 최종적으로 다음과 같은 결과를 얻을 수 있다.
A(나눠질 값) 레지스터 : 0000 0000
B(나누는 값) 레지스터 : 0000 0010
C(나머지) 레지스터 : 0000 0000
D(몫) 레지스터 : 0100 0011
이처럼 나눗셈 연산 회로는 복잡하지만,
산술/논리 연산 회로와 메모리 회로(레지스터)를 통해 구현할 수 있다.
< 산술/논리 연산 회로와 메모리회로의 한계점 >
그런데 연산 자체는 자동으로 진행되는 반면,
사용자는 여전히 각 장치의 연산 결과를 직접 확인하고,
그 결과를 다른 장치에 수동으로 입력해주어야 하는 한계점이 있다.
따라서
이를 극복하기 위해 장치와 다른 장치와의 연결을 자동화하고
동기화하는 제어장치와 클럭이 도입되었다.
이는 메모리 회로 이후 컴퓨터 발전에 중요한 전환점이 되었다.
따라서 다음 주제로 제어장치와 클럭에 대해 탐구해 보겠다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 컴퓨터&과학]' 카테고리의 다른 글
| [컴퓨터][23] 제어장치 - 2 ( JK플립플롭과 클럭) (2) | 2024.09.22 |
|---|---|
| [컴퓨터][22] 제어장치 - 1 (디코더 그리고 산술/논리 장치(ALU : Arithmetic and Logical Unit )) (0) | 2024.09.18 |
| [컴퓨터][20] 메모리 회로 - 2 (바이트와 출력 제어기 그리고 레지스터 : Byte , Enabler , Register ) (0) | 2024.09.12 |
| [컴퓨터][19] 메모리 회로 - 1 (SR 래치(S-R latch), D 래치(D latch), JK플립플롭) (0) | 2024.09.10 |
| [컴퓨터][18] 초기의 컴퓨터 : 산술/논리 연산 회로 총정리 (산술/논리 연산 회로 1~5) (0) | 2024.09.07 |