※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다
이전 글을 통해서
NAND 게이트만을 이용하여
NOT, AND, OR 게이트를 구현해 보았다.
[컴퓨터][10] NAND 게이트 변환 - 1 ( NOT, AND, OR )
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다이전 글을 통해서논리 게이트들을 간편히 표현하기 위한게이트 기호들에 대해 알아보았다. [컴퓨터][9] 논리 게이
core-basic.tistory.com
이어서 NAND 게이트만으로
나머지 게이트들, NOR, XOR, XNOR 등을 구현해 보겠다.
< NAND 게이트 변환 >
( NOR, XOR, XNOR )
< NAND 게이트 >
NAND 게이트의 논리표를 다시 한번 살펴보면 아래와 같다.
| A | B | A NAND B |
| 거짓(0) | 거짓(0) | 참(1) |
| 거짓(0) | 참(1) | 참(1) |
| 참(1) | 거짓(0) | 참(1) |
| 참(1) | 참(1) | 거짓(0) |
그리고 논리표에 따른 NAND 게이트의 회로는 아래와 같다.
< 1 NAND 1 >
< NAND 게이트만으로 NOR 게이트 구현하기>
NAND 게이트의 논리표와 NOT게이트의 논리표를 비교해 보면
아래의 표와 같다.
| A | B | A NAND B | A NOR B |
| 거짓(0) | 거짓(0) | 참(1) | 참(1) |
| 거짓(0) | 참(1) | 참(1) | 거짓(0) |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
| 참(1) | 참(1) | 거짓(0) | 거짓(0) |
이미 앞서서 NAND게이트만으로 OR게이트와 NOT게이트를 구현하였다.
따라서 NAND 게이트로 구현한 OR게이트와 NOT게이트를 연결해 주면
NOR 게이트를 구현할 수 있다.
(※ 이때 전류의 충돌을 방지하기 위해 상황에 맞게 전지의 방향에 변화를 주어 설계한다.)
< 0 NOR 0 == (NOT 0) OR (NOT 0) >
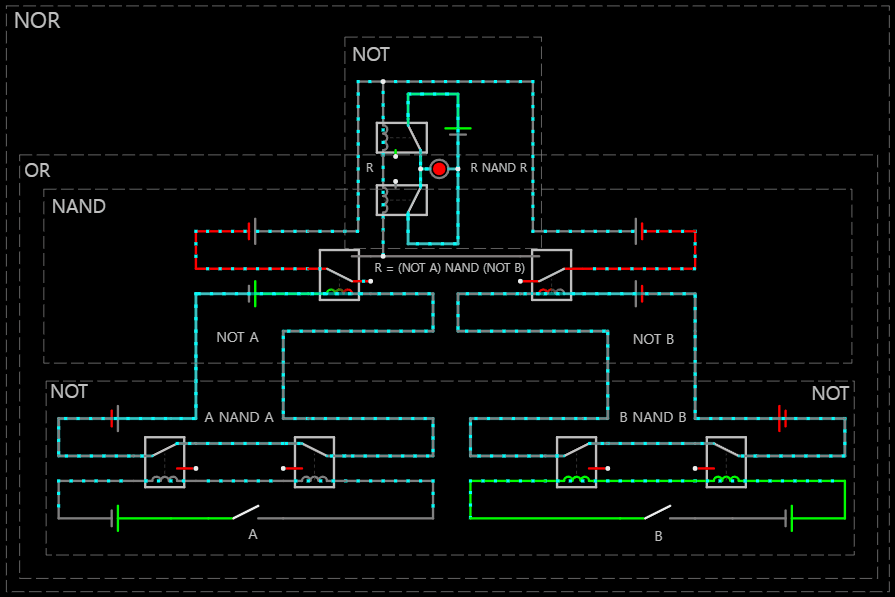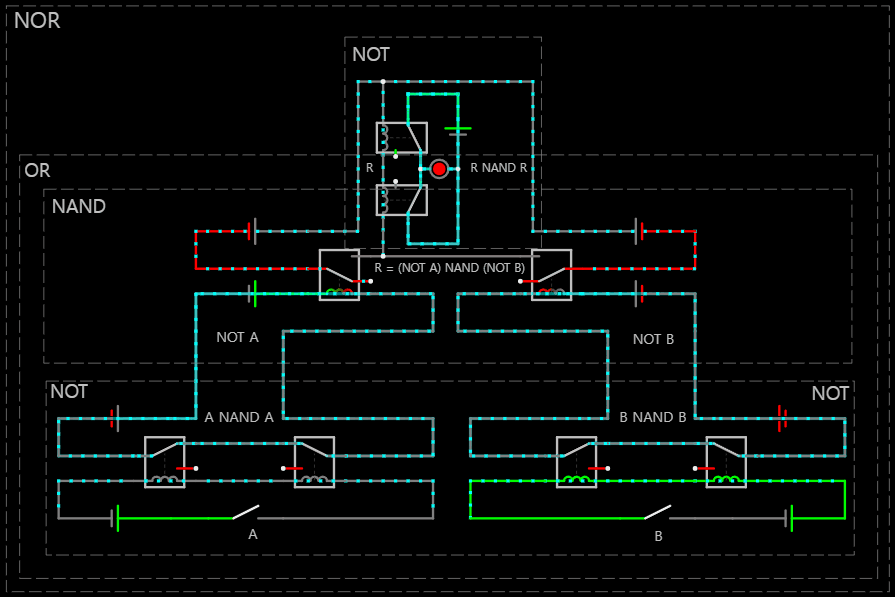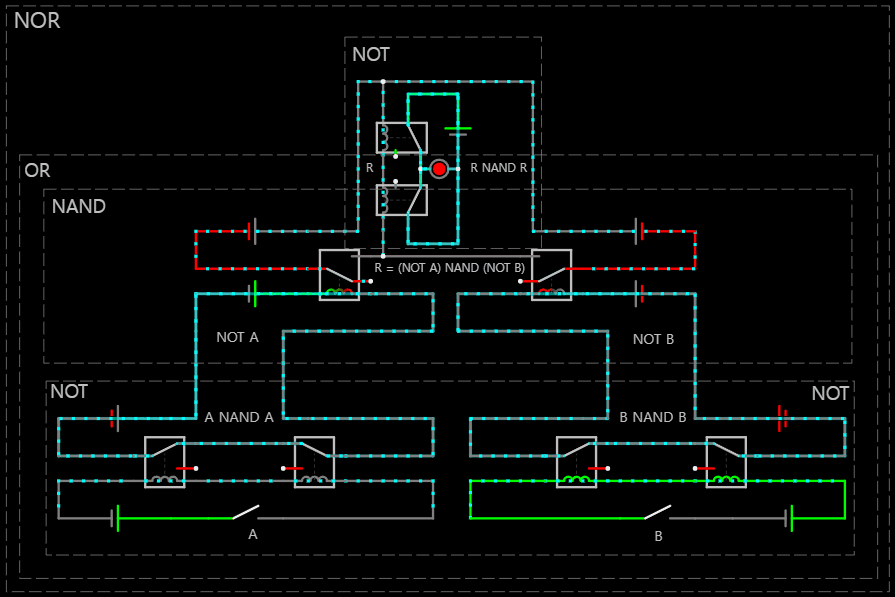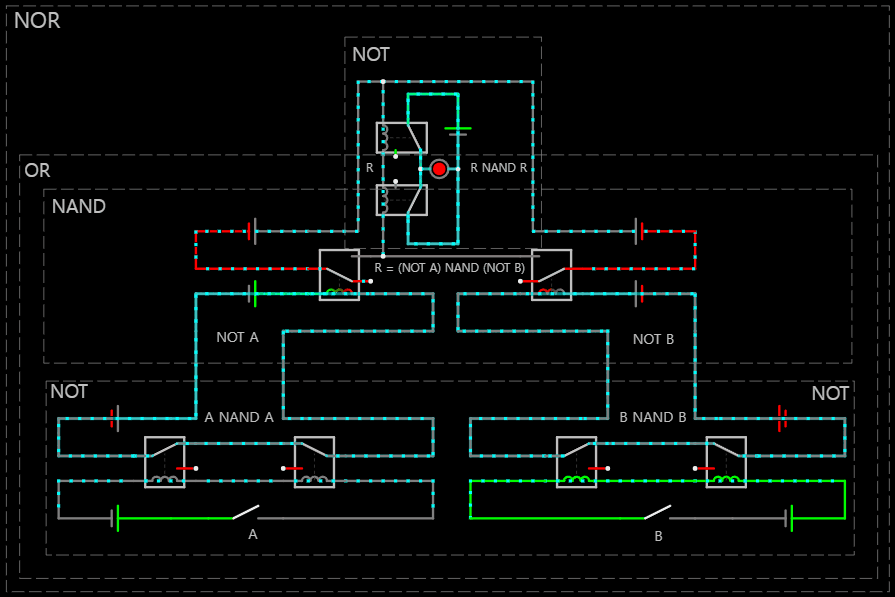
< 0 NOR 1 == (NOT 0) OR (NOT 1) >
< 1 NOR 0 == (NOT 1) OR (NOT 0) >
< 1 NOR 1 == (NOT 1) OR (NOT 1) >
그리고 이를 게이트 기호로 표현하면 아래와 같다.
< NAND 게이트만으로 XOR 게이트 구현하기 >
NAND 게이트의 논리표와 XOR게이트의 논리표를 비교해 보면
아래의 표와 같다.
| A | B | A NAND B | A XOR B |
| 거짓(0) | 거짓(0) | 참(1) | 거짓(0) |
| 거짓(0) | 참(1) | 참(1) | 참(1) |
| 참(1) | 거짓(0) | 참(1) | 참(1) |
| 참(1) | 참(1) | 거짓(0) | 거짓(0) |
A XOR B = [A OR (NOT B)] AND [(NOT A) OR B] 따른다.
이미 앞서서 NAND게이트만으로 AND, OR, NOT게이트를 구현하였기에
XOR 게이트도 위의 식에 따라 구현할 수 있다.
하지만, 매우 복잡한 형태이다.
따라서, NAND 게이트만으로 XOR을 구현하는 또 다른 간단한 형태가 존재한다.
[A NAND (A NAND B)] NAND [(A NAND B) NAND B]
| A | B | A NAND B | A NAND (A NAND B) | (A NAND B) NAND B |
| 거짓(0) | 거짓(0) | 참(1) | 참(1) | 참(1) |
| 거짓(0) | 참(1) | 참(1) | 참(1) | 거짓(0) |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) | 참(1) |
| 참(1) | 참(1) | 거짓(0) | 참(1) | 참(1) |
| [A NAND (A NAND B)] NAND [(A NAND B) NAND B] | A XOR B |
| 거짓(0) | 거짓(0) |
| 참(1) | 참(1) |
| 참(1) | 참(1) |
| 참(1) | 참(1) |
(※ 이때 전류의 충돌을 방지하기 위해 상황에 맞게 전지의 방향에 변화를 주어 설계한다.)
< 0 XOR 0 >
[0 NAND (0 NAND 0)] NAND [(0 NAND 0) NAND 0]
< 0 XOR 1 >
[0 NAND (0 NAND 1)] NAND [(0 NAND 1) NAND 1]
< 1 XOR 0 >
[1 NAND (1 NAND 0)] NAND [(1 NAND 0) NAND 0]
< 1 XOR 1 >
[1 NAND (1 NAND 1)] NAND [(1 NAND 1) NAND 1]
그리고 이를 게이트 기호로 표현하면 아래와 같다.
< NAND 게이트만으로 XNOR 게이트 구현하기 >
NAND 게이트의 논리표와 XNOR게이트의 논리표를 비교해 보면
아래의 표와 같다.
| A | B | A NAND B | A XNOR B |
| 거짓(0) | 거짓(0) | 참(1) | 참(1) |
| 거짓(0) | 참(1) | 참(1) | 거짓(0) |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
| 참(1) | 참(1) | 거짓(0) | 참(1) |
이미 앞서서 NAND게이트만으로 XOR게이트와 NOT게이트를 구현하였다.
따라서 NAND게이트로 구현한 XOR게이트와 NOT게이트를 연결해 주기만 하면
XNOR 게이트를 구현할 수 있다.
| A | B | A NAND B | A XOR B | NOT (A XOR B) | A XNOR B |
| 거짓(0) | 거짓(0) | 참(1) | 거짓(0) | 참(1) | 참(1) |
| 거짓(0) | 참(1) | 참(1) | 참(1) | 거짓(0) | 거짓(0) |
| 참(1) | 거짓(0) | 참(1) | 참(1) | 거짓(0) | 거짓(0) |
| 참(1) | 참(1) | 거짓(0) | 거짓(0) | 참(1) | 참(1) |
(※ 이때 전류의 충돌을 방지하기 위해 상황에 맞게 전지의 방향에 변화를 주어 설계한다.)
< 0 XNOR 0 = NOT (0 XOR 0) >
NOT [{0 NAND (0 NAND 0)} NAND {(0 NAND 0) NAND 0}]
< 0 XNOR 1 = NOT (0 XOR 1) >
NOT [{0 NAND (0 NAND 1)} NAND {(0 NAND 1) NAND 1}]
< 1 XNOR 0 = NOT (1 XOR 0) >
NOT [{1 NAND (1 NAND 0)} NAND {(1 NAND 0) NAND 0}]
< 1 XNOR 1 = NOT (1 XOR 1) >
NOT [{1 NAND (1 NAND 1)} NAND {(1 NAND 1) NAND 1}]
그리고 이를 게이트 기호로 표현하면 아래와 같다.
< 컴퓨터의 모든 회로는 NAND 게이트 >
결국 NAND 게이트로 AND, OR, NOT, XOR, NAND, NOR, XNOR 등
모든 부울 연산자, 논리 게이트를 구현할 수 있다.
이는 결국 컴퓨터의 모든 회로는 NAND 게이트로 구현된다고 볼 수 있다.
또한, NAND 게이트만 사용하면 되기 때문에
경제적인 측면에서 비용을 절감할 수 있을 뿐만 아니라,
회로의 최적화와 성능 측면에서도 효율적임을 알 수 있다.
이번 글은 요기서 마치며, 다음 주제로는
그래서, 게이트를 통해서 어떻게 컴퓨터를 구현할 수 있는지 탐구해 보겠다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다
'[無에서 시작하는 컴퓨터&과학]' 카테고리의 다른 글
| [컴퓨터][13] 산술/논리 연산 회로 - 1 (이진법과 비트 그리고 덧셈 회로 : 반가산기) (0) | 2024.08.30 |
|---|---|
| [컴퓨터][12] 게이트로 컴퓨터를 구현한다는 것은 어떤 의미인가 (폰 노이만 구조) (0) | 2024.08.28 |
| [컴퓨터][10] NAND 게이트 변환 - 1 ( NOT, AND, OR ) (0) | 2024.08.26 |
| [컴퓨터][9] 논리 게이트 기호 (AND, OR, XOR, NOT, NAND, NOR, XNOR) (0) | 2024.08.25 |
| [컴퓨터][8] 스위치와 릴레이 회로 그리고 NAND, NOR, XNOR 게이트 (0) | 2024.08.24 |