※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서
컴퓨터는 초기에 산술/논리 연산 등 수학적 계산을 자동화하고자
설계되었다는 것을 알게 되었다.
이에 따라, 산술/논리 연산 회로를 구성하는데 어떤 회로가 필요한지
파악하고자 기본적인 산술 연산 회로에 대해 알아보았다.
그래서, 기본적인 산술 연산 중 덧셈과 뺄셈 회로를 구현해 보았고,
그 결과, 산술/논리 연산 회로에는
논리 게이트와 가산기 정도가 필요하다는 것을 알게 되었다.
[컴퓨터][15] 산술/논리 연산 회로 - 3 (뺄셈 회로와 2의 보수)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서컴퓨터는 초기에 산술/논리 연산 등 수학적 계산을 자동화하고자 설계되었음에 따라, 기본적인
core-basic.tistory.com
그러면 이어서 기본적인 산술 연산 중
곱셈 연산 회로를 구현해 보면서,
산술/논리 연산회로에 또 어떤 회로가 필요한지 탐구해 보겠다.
< 산술/논리 연산 회로 (4) >
(곱셈 회로와 시프트(Shift) 연산)
< 이진수의 곱셈 과정 >
이진수의 곱셈 과정은 십진수의 곱셈 과정과 같다.
다만, 십진수는 0x0~9x9까지의 모든 곱셈을 파악해야 하지만,
이진수는 0x0~1x1, 단 두 개의 숫자만 파악하면 된다.
따라서,
1bit 이진수의 곱셈 연산의 모든 경우의 수를 살펴보면 다음과 같다.
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
이를 논리 게이트와 비교하면 AND게이트와 같다는 사실을 먼저 확인할 수 있다.
그래서
이를 바탕으로 8bit 곱셈 연산 과정에 대해, 3x3=9를
계산하는 예시를 들면 다음과 같다.
|0000 0011 (3)
× |0000 0011 (3)
--------------------------------------------
|0000 0011
0|0000 0110
00|0000 0000
000|0000 0000 0000
0 0000|0000 0000
00 0000|0000 0000
000 0000|0000 0000
--------------------------------------------
000 0000|0000 1001 (9)
과정을 풀어서 설명하면
(1)
피연산자의 첫 번째 이진수와 두 번째 이진수의 첫 번째 자릿수와 AND 연산한 후,
피연산자의 첫 번째 이진수의 모든 비트를 왼쪽으로 이동시킨다.
( 0000 0011 → 0000 0110 )
(2)
이동된 첫 번째 이진수와 두 번째 이진수의 두 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 0000 0110 → 0000 1100 )
(3)
이동된 첫 번째 이진수와 두 번째 이진수의 세 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 0000 1100 → 0001 1000 )
(4)
이동된 첫 번째 이진수와 두 번째 이진수의 네 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 0001 1000 → 0011 0000 )
(5)
이동된 첫 번째 이진수와 두 번째 이진수의 다섯 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 0011 0000 → 0110 0000 )
(6)
이동된 첫 번째 이진수와 두 번째 이진수의 여섯 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 0110 0000 → 1100 0000 )
(7)
이동된 첫 번째 이진수와 두 번째 이진수의 일곱 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 1100 0000 → 1000 0000 )
(8)
이동된 첫 번째 이진수와 두 번째 이진수의 여덟 번째 자릿수와 AND 연산한 후,
이동된 첫 번째 이진수를 모든 비트를 또 왼쪽으로 이동시킨다.
( 1000 0000 → 0000 0000 )
(9)
모든 AND 연산 결과를 합하여 결과를 출력한다.
이때 실질적인 회로 출력 결과는 하위 8bit만 해당된다.
따라서
덧셈 회로는 이미 구현하였으므로,
곱셈 연산 과정의 핵심은 “어떻게 모든 비트를 왼쪽으로 이동시키는가?”라는
질문의 해결과도 같다.
< 시프트(Shift) 연산 회로 >
주어진 비트들을 왼쪽으로 또는 오른쪽으로 이동시키는 연산을
시프트(shift) 연산이라고 한다.
왼쪽으로 이동시키는 경우 SHL (Shift Left) 연산,
오른쪽으로 이동시키는 경우 SHR (Shift Right) 연산이라고 부른다.
이를 회로로 구현하는 간단한 방법은 다음 그림과 같이
입력과 출력을 연결시키는 전선을 한 칸씩 이동시키면 된다.
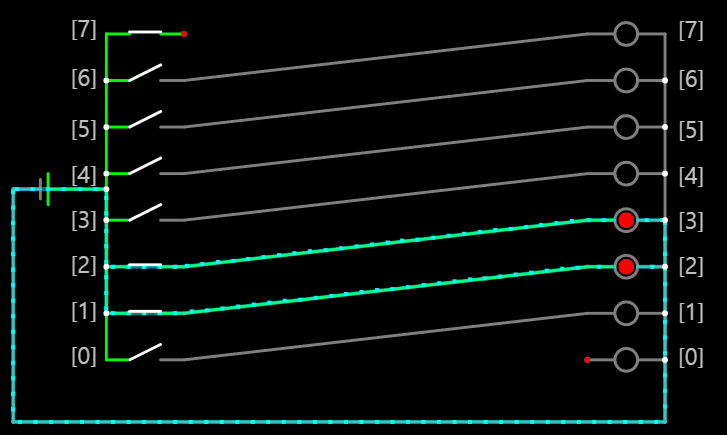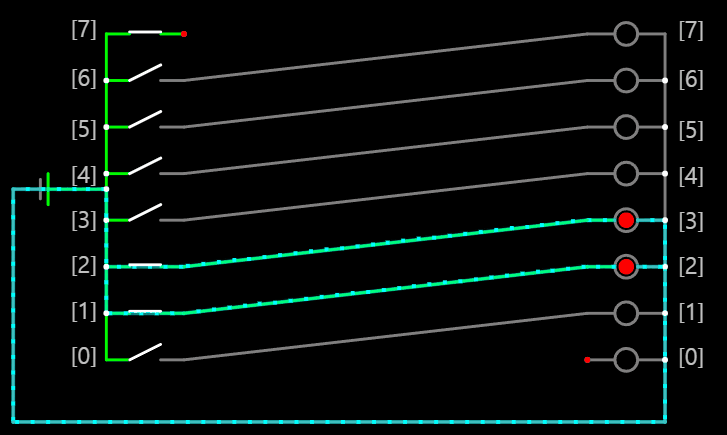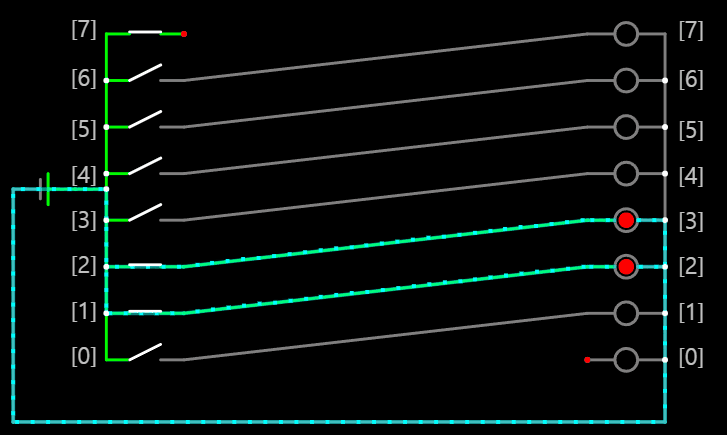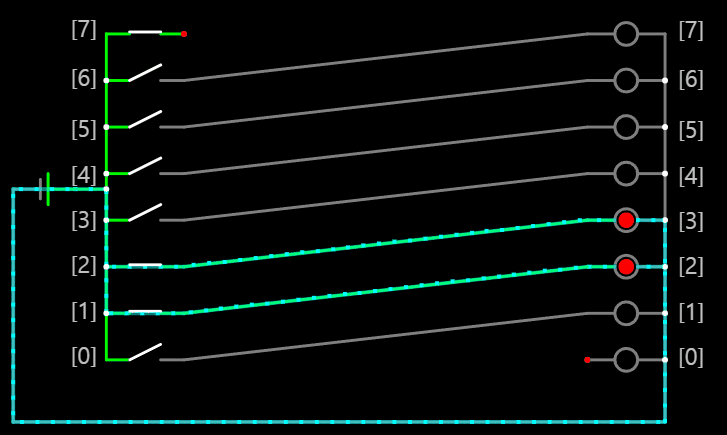
이처럼 0000 0110 입력 결과 0000 1100이라는 결과를 얻을 수 있다.
하지만,
입력의 마지막 비트와, 출력의 첫 번째 비트가 아무것도 연결되어 있지 않다.
이에 대해서,
필자의 주관적인 생각은 만약
입력의 마지막 비트와, 출력의 첫 번째 비트를 연결시키면
왼쪽 회전 연산(Rotate Left)을 하게 된다.
하지만
이는 곱셈 연산에 사용되지 않는 연산이다.
그런데 만약 하나의 입력 비트를 더 추가하고,
이를 입력의 마지막 비트와 AND 연산 후에,
출력의 첫 번째 비트와 연결시켜 주면,
연결되지 않은 부분도 없고,
회전 연산과, 시프트 연산 모두 가능할 수 있다고 보았다.
따라서 이를 회로로 표현하면 다음과 같으며, 예시로 1000 0110 값을 입력하였다.
[ Shift Left ]
1000 0110 → 0000 1100

[ Rotate Left ]
1000 0110 → 0000 1101

또한 주어진 이진수를 한 번 왼쪽 시프트 할 때 ×2와 같은 값이 된다.
그리고, 주어진 이진수를 한 번 오른쪽 시프트 ÷2와 같은 값이 된다.
< 시프트 회로 기호(symbol) >
논리 게이트 기호(symbol)와 같이,
시프트 연산 회로도 다음과 같은 기호로 표기할 수도 있다.
 |
 |
< 곱셈 과정 >
따라서 위의 과정을 토대로
4bit 곱셈 0011 (3) x 0011(3) = 1001 (9) 연산 과정을
논리게이트와 가산기 그리고,
시프트 연산 회로를 통해 표현하면 다음과 같다.
| (1) 0011 x 0011 (2) 0011 AND (3) SHL 0011 → 0110 (4) 0110 AND (5) SHL 0110 → 1100 (6) 1100 AND (7) SHL 1100 → 1000 (8) 0110 AND 0 (9) ADD (O₁, O₂) → 0011 + 0110 = 1001(p) (10) ADD (p , O₃) → 1001 + 0000 = 1001(q) (11) ADD (q , O₄) → 1001 + 0000 = 1001 따라서 최종 출력 결과는 0011 (3) x 0011(3) = 1001 (9)가 된다. |
< 4x4 곱셈 회로 >
입출력 4bit인 4x4곱셈회로는 다음과 같으며 예시로 앞선
<곱셈 과정> : 0011 (3) x 0011(3) = 1001 (9) 계산을 확인할 수 있다.

< 곱셈 회로와 산술/논리 연산회로 >
곱셈 회로의 중요한 핵심은 결국
논리 게이트와 덧셈회로(가산기) 그리고,
시프트(shift) 회로가 필요하다는 것이다.
이를 통해 산술/논리 연산 회로를 구현하기 위해서는
기본적으로 논리 게이트 회로와 가산기 회로 그리고
시프트 회로도 필요하다는 것을 알게 되었다.
하지만 초기의 컴퓨터에서
곱셈 연산은 위와 같이
덧셈을 반복하는 방식으로 처리되었는데
이에 따라 덧셈/뺄셈 회로 처럼
다른 연산과 동일한 회로에서 구현되지는 못했다.
따라서 독립적인 회로로 사용할 수 밖에 없었다.
이번 글은 요기서 마치며,
다음 글은 산술 연산 회로 중 나눗셈 회로에 대해 알아보면서
궁극적으로 산술/논리 연산에 어떤 회로가 필요한지 탐구해 보겠다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 컴퓨터&과학]' 카테고리의 다른 글
| [컴퓨터][18] 초기의 컴퓨터 : 산술/논리 연산 회로 총정리 (산술/논리 연산 회로 1~5) (0) | 2024.09.07 |
|---|---|
| [컴퓨터][17] 산술/논리 연산 회로 - 5 (나눗셈 회로와 비교 연산 그리고 메모리) (0) | 2024.09.05 |
| [컴퓨터][15] 산술/논리 연산 회로 - 3 (뺄셈 회로와 2의 보수) (1) | 2024.09.02 |
| [컴퓨터][14] 산술/논리 연산 회로 - 2 (덧셈 회로 : 전가산기, 8bit 전가산기) (1) | 2024.09.01 |
| [컴퓨터][13] 산술/논리 연산 회로 - 1 (이진법과 비트 그리고 덧셈 회로 : 반가산기) (0) | 2024.08.30 |