※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서
컴퓨터는 초기에 산술/논리 연산 등 수학적 계산을 자동화하고자
설계되었다는 것을 알게 되었다.
이에 따라, 산술/논리 연산 회로를 구성하는데 어떤 회로가 필요한지
파악하고자, 기본적인 산술 연산 회로에 대해 알아보았다.
그래서, 덧셈, 뺄셈, 곱셈 회로까지 구현해 보았고,
그 결과 산술 논리 연산 회로에는,
AND, OR, XOR, NOT 게이트 그리고, 가산기와 시프트 연산 회로가
필요하다는 것을 알게 되었다.
[컴퓨터][16] 산술/논리 연산 회로 - 4 (곱셈 회로와 시프트(Shift) 연산)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서컴퓨터는 초기에 산술/논리 연산 등 수학적 계산을 자동화하고자 설계되었다는 것을 알게 되었
core-basic.tistory.com
그러면 이어서 기본적인 산술 연산인 덧셈, 뺄셈, 곱셈, 나눗셈 중
마지막 연산인 나눗셈 연산에 대해 회로를 구현해 보면서,
산술/논리 연산회로에 또 어떤 회로가 필요한지 탐구해 보겠다.
< 산술/논리 연산 회로 (5) >
(나눗셈 회로와 비교 연산 그리고 메모리)
< 십진수의 나눗셈 과정 >
우선 나눗셈의 원리에 대해
십진수로 예를 들어 설명하면
123 ÷ 3에 대해
(1)
123 가장 큰 자리 1을 3으로 나눈다.
1 ÷ 3 = 0x3 + 1
(2)
3으로 나누지 못하기 때문에 몫의 왼쪽에서 첫 번째 자리는 0이며 나머지는 1이 된다.
(3)
이후 나머지에 다음 자리 '2'를 붙여서 나머지에 대해 나눗셈을 진행한다.
12 ÷ 3 = 4x3 + 0
(4)
3으로 나눌 수 있기 때문에 몫의 왼쪽에서 두 번째 자리는 4이며, 나머지는 0이 된다.
(5)
이후 나머지에 다음 자리 '3'를 붙여서 나머지에 대해 나눗셈을 진행한다.
3 ÷ 3 = 1x3 + 0
(6)
3으로 나눌 수 있기 때문에 몫의 왼쪽에서 세 번째 자리는 1이며, 나머지는 0이 된다.
따라서 더 이상 나머지에 붙일 다음자리가 없으므로,
최종 결과는 123 ÷ 3 = 041 + 0 = 41이 된다.
따라서 나눗셈의 핵심은
각 자리에서 나누지 못한 나머지를 다음 자리 숫자와 결합해 계속 나누는 것이다.
그리고 나눗셈에서 몫은 몇 번 뺄 수 있느냐라는 질문과 동일하다.
십진수는 각 자리에서 최대 0부터 9번까지 뺄 수 있다.
만약 10번이 넘어간다면 이전에 이미 상위 자리에서 뺐어야 했다.
이에 대해 이진수는
0과 1밖에 없다.
따라서 이진수의 나눗셈에서는
몫에도 0과 1밖에 올 수 없으며 이는
각 자리에서 0번 빼거나 1번 빼거나 밖에 할 수 없다.
따라서 한 번의 뺄셈만 사용해도, 나눗셈과 같은 효과를 얻을 수 있다.
< 이진수의 나눗셈 과정 >
그러므로 이진수의 나눗셈 과정은
가장 왼쪽 자리부터 나머지로 보낸 후
나머지와 나누는 값을 비교하여 빼지 못한다면 (= 나누지 못한다면)
몫은 0이 되고,
빼지 못한 나머지는 다음 자리 숫자와 결합하기 위해 시프트 연산을 진행한다.
그리고 다시 그다음 자리를 나머지로 보내며
위의 과정을 반복한다.
이진수의 나눗셈 과정에 대해
4bit 나눗셈 연산 과정을 예시를 들어 설명하면 다음과 같다.
1001 (9) ÷ 0011 (3) = 0011 (3)에 대해서,
[0. 초기화 과정]
몫과 나머지를 0으로 초기화하고,
나눠질 값 : 1001’, ‘나누는 값 : 0011’의
각 자릿수를 비교하여
‘나눠질 값 : 1001’ > ‘나누는 값 : 0011’인지 확인한다.
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0000 |
[1. 몫의 가장 왼쪽 비트인 네 번째 비트 처리하기 ]
| (1) 나눠질 값 : 1001의 네 번째 비트를 바로 나머지의 첫 번째 비트에 입력한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0001 |
| (2) 나머지와 나누는 값을 비교하여, 나머지가 더 작을 경우 즉, 0001 < 0011 일 경우 몫의 마지막, 네번째 비트가 0이 된다 |
|
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0001 |
| (3) 이후, 나머지를 왼쪽으로 시프트 연산한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0001 → 0010 |
[2. 몫의 세 번째 비트 처리하기 ]
| (1) 나눠질 값 : 1001의 세 번째 비트를 나머지의 첫 번째 비트에 입력한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0010 |
| (2) 나머지와 나누는 값을 비교하여, 나머지가 더 작을 경우 즉, 0010 < 0011 일 경우 몫의 세번째 비트가 0이 된다 |
|
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0001 |
| (3) 이후, 나머지를 왼쪽으로 시프트 연산한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0010 → 0100 |
[3. 몫의 두 번째 비트 처리하기 ]
| (1) 나눠질 값 : 1001의 두 번째 비트를 나머지의 첫 번째 비트에 입력한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0000 |
| 나머지 | 0100 |
| (2) 나머지와 나누는 값을 비교하여, 나머지가 더 크거나, 같으면 즉, 0100 ≥ 0011 일 경우 몫의 두번째 비트가 1이 된다. 그리고 나머지에서 나누는 값을 뺀다. 0100 - 0011 = 0001 |
|
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0010 |
| 나머지 | 0100 - 0011 = 0001 |
| (3) 이후, 나머지를 왼쪽으로 시프트 연산한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0010 |
| 나머지 | 0001 → 0010 |
[4. 몫의 첫 번째 비트 처리하기 ]
| (1) 나눠질 값 : 1001의 첫 번째 비트를 나머지의 첫 번째 비트에 입력한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0010 |
| 나머지 | 0011 |
| (2) 나머지와 나누는 값을 비교하여, 나머지가 더 크거나, 같으면 즉, 0011 ≥ 0011 일 경우 몫의 첫번째 비트가 1이 된다. 그리고 나머지에서 나누는 값을 뺀다. 0011 - 0011 = 0000 |
|
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0011 |
| 나머지 | 0011- 0011 = 0000 |
| (3) 이후, 나머지를 왼쪽으로 시프트 연산한다. | |
| 나눠질 값 | 1001 |
| 나누는 값 | 0011 |
| 몫 | 0011 |
| 나머지 | 0000 |
따라서 더 이상 나머지에 붙일 다음자리가 없으므로,
최종 결과는 1001 ÷ 0011 = 0011(몫) × 0011 + 0(나머지) 이 된다.
< 나눗셈 연산 회로 >
따라서 위의 나눗셈 과정을 회로로 구현하기 위해서는
뺄셈 회로 (논리 게이트 + 가산기),
시프트 연산 회로,
두 이진수를 비교 연산하는 회로,
몫과 나머지를 저장하고 재활용할 수 있는 회로,
등이 필요하다.
그런데
뺄셈 회로와, 시프트 회로는 앞선 글을 통해서 구현하였지만,
두 이진수를 비교 연산하는 회로와
몫과, 나머지를 저장할 수 있는 회로는 아직 구현하지 못했다.
따라서 현재까지 파악한 회로들로는 나눗셈 회로를 구현할 수 없다.
그러므로 우선 두 이진수를 비교 연산하는 회로에 대해 알아보겠다.
< 비교 연산 회로 >
비교 연산 회로는 다음과 같은 관계를 판단하는 데 사용된다.
첫 번째는 두 개의 입력값이 같은가.
두 번째는 두 개의 입력값이 다른가.
세 번째는 두 개의 입력값 A, B에 대해서 A가 더 큰가(= A가 더 작은가)
이에 대해 1x1 비교 연산 과정을 예시를 들어
비교 연산 회로가 어떻게 구현되는지 알아보겠다.
< 1 x 1 비교 연산 회로 >
1bit 크기를 가지는 A, B에 대해서
비교 연산을 할 경우, 모든 경우의 수를 살펴보면 다음과 같다.
| A | B | A = B | A ≠ B | A > B |
| 0 | 0 | 참(1) | 거짓(0) | 거짓(0) |
| 0 | 1 | 거짓(0) | 참(1) | 거짓(0) |
| 1 | 0 | 거짓(0) | 참(1) | 참(1) |
| 1 | 1 | 참(1) | 거짓(0) | 거짓(0) |
그리고 주어진 표를 논리 게이트와 비교하면
A = B의 결과는 A, B에 대해서 XNOR 또는 XOR + NOT게이트와 같고,
A ≠ B의 결과는 A, B에 대해서 XOR 게이트와 같다.
A > B의 결과는 A≠B를 확인한 후에 A > B를 계산할 수 있다.
따라서, A ≠ B가 참(1)인 경우에만 A를 확인하여 A > B를 판별할 수 있으므로,
A≠B, A에 대해서, 논리 게이트와 비교하면 (A XOR B) AND A 게이트와 같다.
따라서 이를 논리 게이트 표에 대응시키면 다음과 같다.
| A | B | NOT(A XOR B) A = B |
A XOR B A ≠ B |
(A XOR B) AND A A > B |
| 0 | 0 | 참(1) | 거짓(0) | 거짓(0) |
| 0 | 1 | 거짓(0) | 참(1) | 거짓(0) |
| 1 | 0 | 거짓(0) | 참(1) | 참(1) |
| 1 | 1 | 참(1) | 거짓(0) | 거짓(0) |
이를 논리 게이트를 통해 회로로 구현하면 다음과 같다.
< (A, B) = (0, 0) >
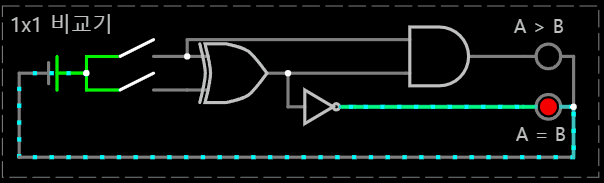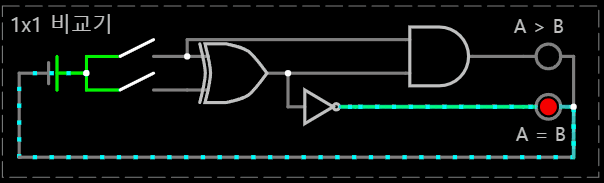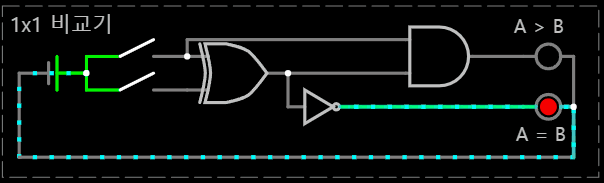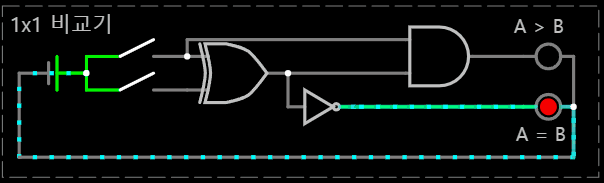
< (A, B) = (0, 1) >
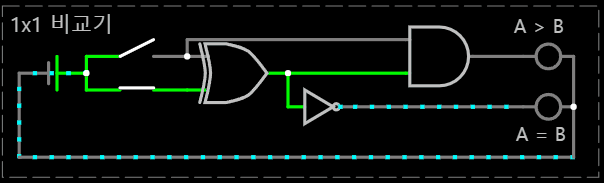
< (A, B) = (1, 0) >
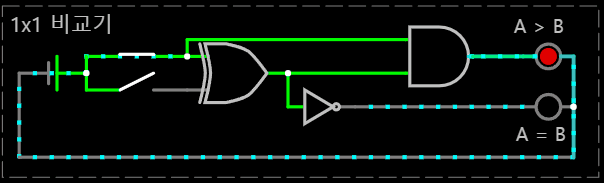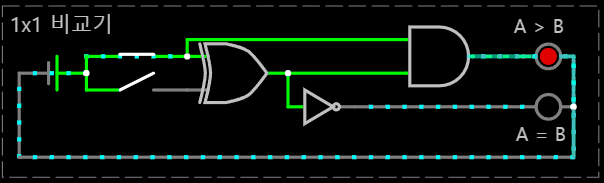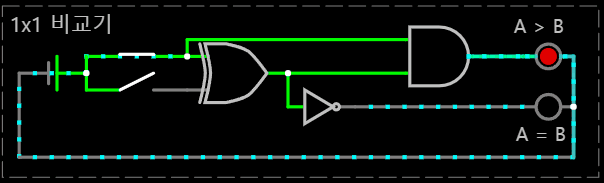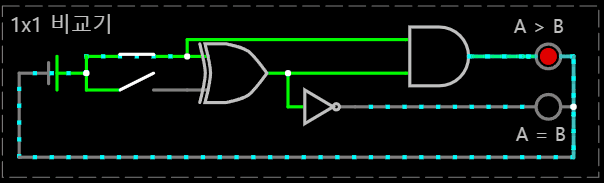
< (A, B) = (1, 1) >
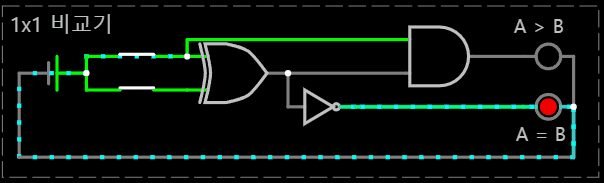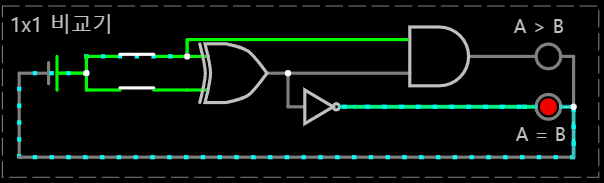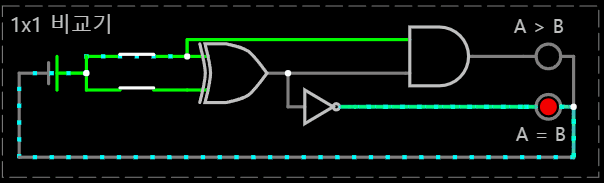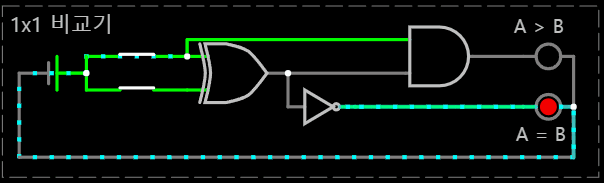
< N x N 비교 연산 회로 >
1 x 1 비교 연산 회로를 확장하여
N x N 비교 연산 회로를 구현하기 위해서는
현재 비트의 비교 연산뿐만 아니라,
상위 비트와 비교 연산을 고려해서 결과를 출력해야 한다.
따라서
N x N 비교 연산 회로 중 가장 간단한 예시인 2bit A, B 비교 연산에 대해서
A, B가 다음과 같을 때
A = [A₁][A₀]
B = [B₁][B₀]
[A ₁]과 [B₁]은 이미 1x1 비교 회로를 통해 결과가 나왔고,
이후 [A₀]와 [B₀]를 비교하는 상황에서
발생되는 모든 경우의 수 살펴보면 다음과 같다.
< 0 = A₁ = B₁ : 참(1) / A₁ > B₁ : 거짓(0) >
| [A₁] = [B₁] = 0 | [A₁] > [B₁] | [A₀] | [B₀] |
| 참(1) | 거짓(0) | 0 | 0 |
| 참(1) | 거짓(0) | 0 | 1 |
| 참(1) | 거짓(0) | 1 | 0 |
| 참(1) | 거짓(0) | 1 | 1 |
| [A₀] = [B₀] | [A₀] > [B₀ | [A₁][A₀] = [B₁][B₀] | [A₁][A₀] > [B₁][B₀] |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
| 거짓(0) | 거짓(0) | 거짓(0) | 거짓(0) |
| 거짓(0) | 참(1) | 거짓(0) | 참(1) |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
< 1 = A₁ = B₁ : 참(1) / A₁ > B₁ : 거짓(0) >
| [A₁] = [B₁] = 1 | [A₁] > [B₁] | [A₀] | [B₀] |
| 참(1) | 거짓(0) | 0 | 0 |
| 참(1) | 거짓(0) | 0 | 1 |
| 참(1) | 거짓(0) | 1 | 0 |
| 참(1) | 거짓(0) | 1 | 1 |
| [A₀] = [B₀] | [A₀] > [B₀ | [A₁][A₀] = [B₁][B₀] | [A₁][A₀] > [B₁][B₀] |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
| 거짓(0) | 거짓(0) | 거짓(0) | 거짓(0) |
| 거짓(0) | 참(1) | 거짓(0) | 참(1) |
| 참(1) | 거짓(0) | 참(1) | 거짓(0) |
< A₁ = B₁ : 거짓(0) / A₁ > B₁ : 거짓(0) >
| [A₁] = [B₁] | [A₁] > [B₁] | [A₀] | [B₀] |
| 거짓(0) | 거짓(0) | 0 | 0 |
| 거짓(0) | 거짓(0) | 0 | 1 |
| 거짓(0) | 거짓(0) | 1 | 0 |
| 거짓(0) | 거짓(0) | 1 | 1 |
| [A₀] = [B₀] | [A₀] > [B₀ | [A₁][A₀] = [B₁][B₀] | [A₁][A₀] > [B₁][B₀] |
| 참(1) | 거짓(0) | 거짓(0) | 거짓(0) |
| 거짓(0) | 거짓(0) | 거짓(0) | 거짓(0) |
| 거짓(0) | 참(1) | 거짓(0) | 거짓(0) |
| 참(1) | 거짓(0) | 거짓(0) | 거짓(0) |
[ 상위 비트 조건 : A₁ = B₁ : 거짓(0) / A₁ > B₁ : 참(1) ]
| [A₁] = [B₁] | [A₁] > [B₁] | [A₀] | [B₀] |
| 거짓(0) | 참(1) | 0 | 0 |
| 거짓(0) | 참(1) | 0 | 1 |
| 거짓(0) | 참(1) | 1 | 0 |
| 거짓(0) | 참(1) | 1 | 1 |
| [A₀] = [B₀] | [A₀] > [B₀ | [A₁][A₀] = [B₁][B₀] | [A₁][A₀] > [B₁][B₀] |
| 참(1) | 거짓(0) | 거짓(0) | 참(1) |
| 거짓(0) | 거짓(0) | 거짓(0) | 참(1) |
| 거짓(0) | 참(1) | 거짓(0) | 참(1) |
| 참(1) | 거짓(0) | 거짓(0) | 참(1) |
이에 따라 주어진 표를 논리 게이트와 비교하면
[A₀] = [B₀]의 결과는 A, B에 대해서 XOR+NOT게이트와 같다.
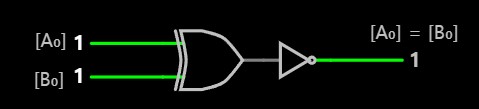
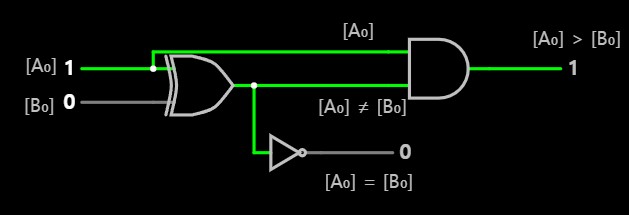
[A₀] > [B₀]의 결과는 [A₀] = [B₀] 확인한 후에 [A₀] > [B₀]를 계산할 수 있다.
따라서,
NOT([A₀] = [B₀])가 참(1)인 경우에만 [A₀]를 확인하여
[A₀] > [B₀]를 판별할 수 있으므로,
NOT(A=B), A에 대해서, 논리 게이트와 비교하면 (A XOR B) AND A 게이트와 같다.
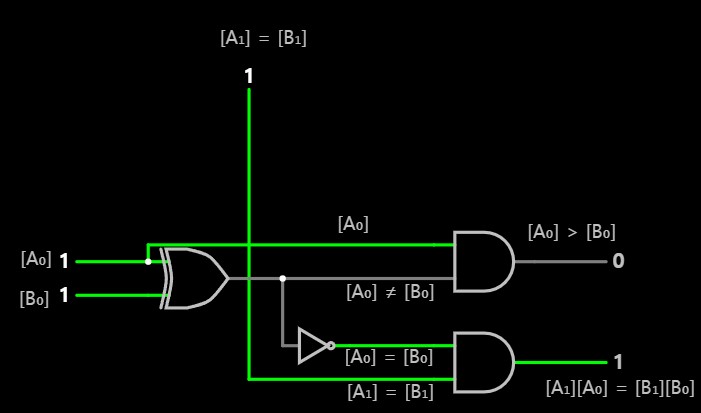
최종 결과인 [A₁][A₀] = [B₁][B₀], [A₁][A₀] > [B₁][B₀]에 대해서
표를 보면 상위 비트의 영향을 받는다는 것을 알 수 있다.
따라서
[A₁][A₀] = [B₁][B₀] 결과는
[A₀] = [B₀]의 결과와, [A₁] = [B₁]의 결과에 대해서 AND 게이트와 같다.
따라서 (NOT(A XOR B)) AND ([A₁] = [B₁]의 결과)와 같다.
[A₁][A₀] > [B₁][B₀] 결과는 우
선 [A₁] = [B₁] 결과를 확인하고 참(1)이면
[A₀] = [B₀] 결과도 확인한 후에야 [A₁][A₀] > [B₁][B₀를 계산할 수 있다.
따라서,
[A₁] ≠ [B₁] 일 경우, [A₁] > [B₁]를 그대로 최종 결과로 출력하거나, 또는
[A₁] = [B₁] 일 경우, [A₀] ≠ [B₀]가 참(1)인 경우에만
[A₀]를 확인하여 [A₀] > [B₀]를 판별할 수 있으므로,
((A₁ XOR B₁) AND A₁) OR (NOT(A₁ XOR B₁) AND (A₀ XOR B₀) AND A₀)
게이트 회로와 같다.

따라서 최종 2x2 비교 연산 회로는 다음과 같다.

< 산술/논리 연산 회로의 한계 : 메모리 회로의 등장 >
하지만 비교 연산 회로를 구현하였음에도
나눗셈 회로는 아직 구현하지 못한다.
왜냐하면 아직 메모리 회로를 구현하지 못했기 때문이다.
다시 초기로 돌아가보면
컴퓨터는 산술/논리 연산 등 수학적 계산을 자동화하는 목적으로 설계되었다.
이번 글까지 포함해서 산술/논리 연산 회로를 구현하는데 필요한 회로는
AND, OR, NOT, XOR 게이트
가산기 회로,
시프트 회로,
비교 연산 회로,
등이 있다는 것을 파악하였다.
하지만 산술/논리 연산 회로만으로는 계산 결과들을 저장하고,
다시 재활용할 수 없다는 한계가 있었다.
특히 위와 같이 나눗셈 회로 구현 과정에서 그 한계를 느낄 수 있었다.
이에 따라 “계산 결과들을 다시 재활용할 수 없을까”라는 질문이
자연스럽게 제기됨으로써 메모리 회로가 등장하게 되었다.
그렇기에 메모리 회로는 컴퓨터 발전과
구성요소에 중요한 핵심이며 집중적으로 탐구할 필요가 있다.
따라서 이번글은 요기서 마치며,
다음 주제는 지금 까지 구현한 산술/논리 연산의 부분 회로들을 정리하고
산술/논리 연산 회로의 한계를 극복시켜 줄
메모리 회로에 대해 탐구해 보며,
컴퓨터의 발전 과정을 따라가 보겠다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 컴퓨터&과학]' 카테고리의 다른 글
| [컴퓨터][19] 메모리 회로 - 1 (SR 래치(S-R latch), D 래치(D latch), JK플립플롭) (0) | 2024.09.10 |
|---|---|
| [컴퓨터][18] 초기의 컴퓨터 : 산술/논리 연산 회로 총정리 (산술/논리 연산 회로 1~5) (0) | 2024.09.07 |
| [컴퓨터][16] 산술/논리 연산 회로 - 4 (곱셈 회로와 시프트(Shift) 연산) (0) | 2024.09.03 |
| [컴퓨터][15] 산술/논리 연산 회로 - 3 (뺄셈 회로와 2의 보수) (1) | 2024.09.02 |
| [컴퓨터][14] 산술/논리 연산 회로 - 2 (덧셈 회로 : 전가산기, 8bit 전가산기) (1) | 2024.09.01 |