※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서 유클리드 기하학 <원론> 1권 48개의 명제 중
명제 17에 대해 알아보았다.
이어서 명제 18에 대해 알아보겠다.
[수학][21] 유클리드 기하학 <원론> 1권 - 18 (명제 17)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서 유클리드 기하학 1권 48개의 명제 중명제 16에 대해 알아보았다.이어서 명제 17에 대해 알아보겠
core-basic.tistory.com
따라서 이번글의 주제는
< 유클리드 기하학 <원론> 제1권 명제 18 >
모든 삼각형에 대해서, 길이가 긴 변일수록 마주 보는 대각의 크기도 크다.
사용되는 공준
- [공준 1] : 두 점이 주어지면 두 점을 연결하는 직선을 그을 수 있다는 규칙
- [공준 3] : 임의의 한 점(A)과 임의의 간격(r)이 주어지면 해당 점(A)을 중심으로 하고, 일정한 간격(r)에 있는 점들로 원을 그릴 수 있다는 규칙
사용되는 명제
- [명제 3] : 길이가 같지 않은 주어진 두 종료된 직선(선분)에 대하여 길이가 긴 선분에서 짧은 선분과 같은 길이만큼 빼기
- [명제 5] : 이등변 삼각형은 두 밑각의 크기는 같고, 같은 두 변에 해당되는 직선이 연장하였을 때 밑각 아래에 있는 각들도 서로 같다.
- [명제 16] : 삼각형의 한 변을 연장하면서 생성되는 외각의 크기는, 반대쪽 내각들의 각각의 크기보다 크다.
[명제 18]
모든 삼각형에 대해서, 길이가 긴 변일수록 마주 보는 대각의 크기도 크다.
※ 증명에 사용된 그림은 알지오매스 사이트를 통해 제작하였습니다.
- 0 -
주어진 삼각형 △ABC에 대해서, 변 AB보다 변 AC가 더 길다고 하자.
(AB < AC)

- 1 -
[명제 3]에 따라 변 AB보다 길이가 더 긴 변 AC 위에
변 AB와 같은 길이를 가진 선분 AD를 그린다.

< 주관적 생각 >
선분 AB와 선분 AC 그리고 길이를 복제하려는 선분 AD 모두점 A를 포함하고 있으므로,
점 A를 중심으로 하고 간격을 AB를 하는 원을 그리면,
[명제 3]을 사용하지 않고 [공준 3]만으로도, 원과 선분 AC 교점을 D라고 하여,
선분 AB와 같은 길이를 가진 선분 AD를 선분 AC위에 그릴 수 있다.
이는 선분 AB와 AC모두 점 A를 중심인 원의 반지름이기 때문이다.
- 2 -
[공준 1]에 따라 점 B와 점 D를 연결하는 선분을 그린다.
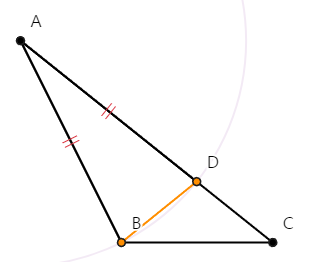
- 3 -
[명제 16]에 따라 △BCD에 대해서,
∠ADB는 외각이므로, 반대쪽 내각인 ∠DCB보다 크다.
( ∠ADB > ∠DCB )
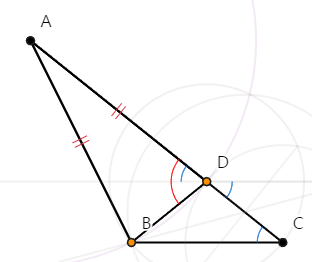
- 4 -
[명제 5]에 따라, △ABD는 이등변 삼각형이므로, ∠ADB = ∠ABD이다.

- 5 -
따라서 (∠ADB=)∠ABD > ∠DCB 부등식이 성립한다.
이때,
∠ABD는 변 AC의 대각인 ∠ABC의 일부분이다.
∠DCB는 변 AB의 대각이다.
따라서
길이가 더 긴 변 AC의 대각 ∠ABC의 일부분인 ∠ABD가
변 AB의 대각 ∠DCB보다 크므로,
변 AC의 대각∠ABC는 변 AB의 대각∠DCB 보다 더 크다.
- 6 -
위와 같은 방법을 통해 모든 삼각형의 길이가 다른 두 변에 대해서,
길이가 긴 변이 마주 보는 대각의 크기도 크다는 것을 확인할 수 있다.
< 주관적 핵심 >
(주관적으로 느낀 핵심)
- 1 -
[명제 18]에 대해서,
삼각형의 길이가 다른 두 변에 대해서
길이가 더 긴 대각의 크기와 길이가 더 짧은 대각의 크기를 비교하기 위해,
같은 선상에 놓아 분명하고, 명백히 비교할 수 있도록 유도했다.
그리고
그렇게 하기 위해 이등변 삼각형을 생성하고, [명제 5], [명제 16]을 활용했다.
특히
[명제 16]은 길이가 더 긴 대각의 크기와 길이가 더 짧은 대각의 크기를
명백히 비교할 수 있도록 결정적인 역할을 하였는데
[명제 16]은 합동과 선분을 이등분하는 점, 그리고
원,
점과 점을 연결하는 직선,
[공리 1], [공리 2], [공리 3] 등
기초적인 정의와 공리, 공준 그리고 증명된 명제까지
이용하였다.
이번 글은 요기서 마치며, 다음 주제는 이어서 1권 명제 19에 대해 탐구할 것 같다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 수학]' 카테고리의 다른 글
| [수학][24] 유클리드 기하학 <원론> 1권 - 21 (명제 20) (0) | 2024.08.17 |
|---|---|
| [수학][23] 유클리드 기하학 <원론> 1권 - 20 (명제 19) (0) | 2024.08.16 |
| [수학][21] 유클리드 기하학 <원론> 1권 - 18 (명제 17) (0) | 2024.08.14 |
| [수학][20] 유클리드 기하학 <원론> 1권 - 17 (명제 16) (0) | 2024.08.13 |
| [수학][19] 유클리드 기하학 <원론> 1권 - 16 (명제 15) (0) | 2024.08.12 |