※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서 유클리드 기하학 <원론> 1권 48개의 명제 중
명제 8에 대해 알아보았다.
이어서 명제 9에 대해 알아보겠다.
[수학][12] 유클리드 기하학 <원론> 1권 - 9 (명제 8)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서 유클리드 기하학 1권 48개의 명제 중명제 7에 대해 알아보았다.이어서 명제 8에 대해 알아보겠다
core-basic.tistory.com
따라서 이번 글의 주제는
< 유클리드 기하학 <원론> 제1권 명제 9 >
주어진 각 이등분 하기
사용되는 공준
- [공준 1] : 두 점이 주어지면 두 점을 연결하는 직선을 그을 수 있다는 규칙
사용되는 명제
- [명제 1] : 종료된 주어진 직선(선분) 위에 정삼각형 그리기
- [명제 3] : 길이가 같지 않은 주어진 두 종료된 직선(선분)에 대하여 길이가 긴 선분에서 짧은 선분과 같은 길이만큼 빼기
- [명제 8] : 두 삼각형에 대해서 대응되는 세 변이 같으면. 두 삼각형은 합동이 되어 대응되는 각들도 모두 같다. (SSS 합동)
[명제 9]
주어진 각 이등분 하기
※증명에 사용된 그림은 알지오매스 사이트를 통해 제작하였습니다.
- 0 -
주어진 각을 ∠BAC라고 하자.
그리고 해당 각을 논리적으로 이등분하고자 한다.

- 1 -
직선 AB위에 임의의 점 D를 잡는다. 그리고
[명제 3]을 이용해, 직선 AC위에 AC보다 짧은 AD와 같은 길이를 가진
선분 AE를 구한다.
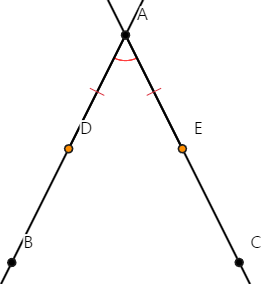
- 2 -
[공준 1]에 따라 점 D와 점 E를 연결하는 선분 DE를 그린다.

- 3 -
[명제 1]에 따라 선분 DE 위에 정삼각형 △DEF을 그린다.

- 4 -
[공준 1]에 따라 점A와 점 F를 연결하여 선분 AF를 그린다.

- 5 -
그러면 [명제 8]에 따라 △ADF, △AEF에 대해서,
선분 AD=선분 AE, 선분 AF는 공통, 선분 DF=EF이므로
△ADF ≡ △AEF 이다.
(SSS합동)
△ADF |
 |
△AEF |
- 6 -
따라서 ∠DAF=∠EAF 이므로
선분 AF가 ∠BAC를 이등분한다.

주관적 핵심
(주관적으로 느낀 숨겨진 핵심)
- 1 -
[명제 9]를 통해서 잊고 있었던 주관적 핵심이 떠올랐다.
명제의 목적이 무엇인지,
그리고 그 목적을 이루기 위해서 어떤 것을 이용했는지,
그리고 어떤 성질을 유도하려 했는지 말이다.
- 2 -
이에 따라 [명제 9]에 대해서
각을 이등분하는데 있어서,
원을 이용해, 정삼각형을 이끌어 냈다.
정삼각형을 이용하므로써, 합동과 대칭성을 이끌어 냈다.
합동과 대칭성을 이용하므로써, 각을 이등분한다.
다시 말하면
각을 이등분 하기 위해,
합동과 대칭성을 이용한다는 것을 알 수 있다.
합동과 대칭성을 이끌어내기 위해,
정삼각형을 이용한다는 것을 알 수 있다.
정삼각형을 이끌어내기 위해,
원을 이용한다는 것을 알 수 있다.
그리고 그 원은 유일한 정의에 따른다.
이를 바탕으로 명제의 핵심들을 종합하는 과정을 재탐구해야겠다는 생각이 들었다.
이번 글은 요기서 마치여, 다음 주제는 이어서 1권 명제 10에 대해 탐구할 것 같다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 수학]' 카테고리의 다른 글
| [수학][15] 유클리드 기하학 <원론> 1권 - 12 (명제 11) (0) | 2024.08.08 |
|---|---|
| [수학][14] 유클리드 기하학 <원론> 1권 - 11 (명제 10) (0) | 2024.08.07 |
| [수학][12] 유클리드 기하학 <원론> 1권 - 9 (명제 8) (0) | 2024.08.05 |
| [수학][11] 유클리드 기하학 <원론> 1권 - 8 (명제 7) (0) | 2024.08.04 |
| [수학][10] 유클리드 기하학 <원론> 1권 - 7 (명제 6) (0) | 2024.08.03 |