※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서 유클리드 기하학 <원론> 1권 48개의 명제 중
명제 20에 대해 알아보았다.
이어서 명제 21에 대해 알아보겠다.
[수학][24] 유클리드 기하학 <원론> 1권 - 21 (명제 20)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서 유클리드 기하학 1권 48개의 명제 중명제 19에 대해 알아보았다.이어서 명제 20에 대해 알아보겠
core-basic.tistory.com
따라서 이번 글의 주제는
< 유클리드 기하학 <원론> 제1권 명제 21 >
삼각형의 변들 중 한 변의 양 끝점으로부터 시작하는 두 직선이
삼각형 내부의 한 점에서 만나도록 하여 새로운 두 변을 생성하면,
새로운 두 변의 길이의 합은
주어진 삼각형의 두 변의 길이의 합보다 작고,
새로운 두 변에 의해 만들어진 각은
주어진 삼각형의 두 변이 이루는 각보다 크다.
사용되는 공리
- [공리 2] : A=B 이면, A+C = B+C이다.
사용되는 공준
- [공준 2] : 이미 주어진 종료된 선(선분)에 대해서 직선으로 연장할 수 있다는 규칙
사용되는 명제
- [명제 16] : 삼각형의 한 변을 연장하면서 생성되는 외각의 크기는, 반대쪽 내각들의 각각의 크기보다 크다.
- [명제 20] : 모든 삼각형에 대해서, 두 변의 길이의 합은 나머지 한 변의 길이보다 더 크다.
[명제 21]
삼각형의 변들 중 한 변의 양 끝점으로부터 시작하는 두 직선이
삼각형 내부의 한 점에서 만나도록 하여 새로운 두 변을 생성하면,
새로운 두 변의 길이의 합은
주어진 삼각형의 두 변의 길이의 합보다 작고,
새로운 두 변에 의해 만들어진 각은
주어진 삼각형의 두 변이 이루는 각보다 크다.
※ 증명에 사용된 그림은 알지오매스 사이트를 통해 제작하였습니다.
- 0 -
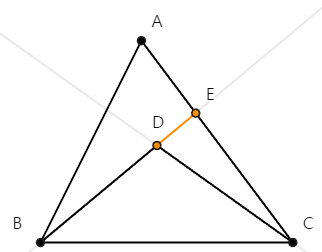
주어진 △ABC에 대해서,
변 BC의 양끝 점인 점 B와 점 C로부터 시작하는 두 직선이
삼각형 내부의 한 점 D에서 만나
새로운 두 변, BD와 CD를 생성한다고 하자.

- 1 -
[공준 2]에 따라 선분 BD를 점 D 방향으로 연장하였을 때,
변 AC와 만나는 점을 E라고 하자.
- 2 -
[명제 20]에 따라, △ABE의 두 변 AB, AE의 길이의 합은
나머지 변 BE보다 크다.
( AB + AE > BE )

- 3 -
[공리 2]에 따라, AB + AE > BE 부등식에서
양변에 EC를 더한
AB + AE + EC > BE + EC 식도 성립한다.
이때 AE+EC = AC이므로
AB + AC > BE + EC 역시 성립한다.

- 4 -
[명제 20]에 따라, △CED의 두 변 EC, ED의 길이의 합은
나머지 변 CD보다 크다.
(EC + ED > CD)

- 5 -
[공리 2]에 따라, EC + ED > CD 부등식에서
양변에 DB를 더한
EC + ED + DB > CD + DB 식도 성립한다.
이때 ED+DB = BE 이므로
EC + BE > CD + DB 역시 성립한다.

- 6 -
앞서 구한 부등식들
AB + AC > BE + EC
EC + BE > CD + DB
이들을 조합하면,
AB + AC > BE + EC > CD + DB
이와 같은 부등식을 얻을 수 있다.
따라서,
새롭게 생성된 두 변 DB, CD길이의 합은 주어진 삼각형의 두 변 AB, AC보다 작다.

- 7 -
각설하여,
[명제 16]에 따르면, 모든 삼각형의 한 변을 연장하면서 생성되는 외각의 크기는,
반대쪽 내각들의 각각의 크기보다 크므로,
△CDE에 대해서 외각 ∠BDC는 반대쪽 내각 ∠CED보다 크다.
( ∠BDC > ∠CED )

- 8 -
또, [명제 16]에 따라
△ABE에 대해서 외각 ∠CEB(=∠CED)는 반대쪽 내각 ∠BAC보다 크다.
( ∠CEB(=∠CED) > ∠BAC )

- 9 -
앞서 구한 부등식들
∠BDC > ∠CED,
∠CEB(=∠CED) > ∠BAC
이들을 조합하면,
∠BDC > ∠CED > ∠BAC
이와 같은 부등식을 얻을 수 있다.
따라서,
새롭게 생성된 두 변 DB, CD가 이루는 각 ∠BDC는
주어진 삼각형의 두 변 AB, AC가 이루는 각 ∠BAC보다 크다.

따라서,
삼각형의 변들 중 한 변의 양 끝점으로부터 시작하는 두 직선이
삼각형 내부의 한 점에서 만나도록 하여 새로운 두 변을 생성하면,
새로운 두 변의 길이의 합은
주어진 삼각형의 두 변의 길이의 합보다 작고,
새로운 두 변에 의해 만들어진 각은
주어진 삼각형의 두 변이 이루는 각보다 크다.
주관적 핵심
(주관적으로 느낀 핵심)
- 1 -
[명제 21] 역시 길이, 크기 등을 비교하는 명제이므로,
그 비교 대상들을 같은 선상에 놓아 분명하고, 명백히 비교할 수 있도록
유도해야 한다.
- 2 -
[명제 20]에서는 각도의 경우 기하학적 그림으로 같은 선상에 놓아
직관적으로 확인할 수 있도록 유도해야 한다고 했지만,
이번 [명제 21]의 증명과정을 보면
이미 증명된 명제들을 사용하여 기하학적 그림이 아닌
비교 대상들이 포함된 등식이나, 부등식을 유도해 냈다.
물론, 이미 증명된 명제들에서 각도의 경우 기하학적 그림으로
같은 선상에 놓아 직관적으로 확인할 수 있도록 유도하였다.
하지만, 지금까지 명제들을 증명하는 과정에서
더 효율적이고, 불필요한 과정을 제거함에 있어서
증명된 명제들을 곧바로 적용시켰다.
이는 논리에 어긋나지 않으므로,
이전에 증명된 명제들을 얼마나 잘 활용하는지도
중요한 핵심이 될 수 있다고 생각한다.
그러나 이미 증명된 명제들도 어떻게 해서 증명이 되었는지
핵심이나 패턴은 알아두면 좋을 것 같다.
- 3 -
어느 순간부터증명의 과정에 대한 핵심에 대한 것만
생각한 것 같다.
증명의 과정뿐만 아니라, 증명의 결과, 명제 자체도
또 다른 명제를 증명하는 데 있어서, 사용될 것이다.
하지만, 명제를 단순히 외운다기보다는
핵심을 파악해야 하는지,
성질을 파악해야 하는지,
어떤 것과의 연관성을 파악해야 하는지,
과연 무엇을 파악하는 것이
명제 자체를 이해하는데 도움이 될지
탐구해 보겠다.
이번 글은 요기서 마치며, 다음 주제는 이어서 1권 명제 22에 대해 탐구할 것 같다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 수학]' 카테고리의 다른 글
| [수학][27] 유클리드 기하학 <원론> 1권 - 24 (명제 23) (0) | 2024.08.20 |
|---|---|
| [수학][26] 유클리드 기하학 <원론> 1권 - 23 (명제 22) (0) | 2024.08.19 |
| [수학][24] 유클리드 기하학 <원론> 1권 - 21 (명제 20) (0) | 2024.08.17 |
| [수학][23] 유클리드 기하학 <원론> 1권 - 20 (명제 19) (0) | 2024.08.16 |
| [수학][22] 유클리드 기하학 <원론> 1권 - 19 (명제 18) (0) | 2024.08.15 |