※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서 유클리드 기하학 <원론> 1권 48개의 명제 중
명제 21에 대해 알아보았다.
이어서 명제 22에 대해 알아보겠다.
[수학][25] 유클리드 기하학 <원론> 1권 - 22 (명제 21)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서 유클리드 기하학 1권 48개의 명제 중명제 20에 대해 알아보았다.이어서 명제 21에 대해 알아보겠
core-basic.tistory.com
따라서 이번 글의 주제는
< 유클리드 기하학 <원론> 제1권 명제 22 >
세 개의 종료된 직선(선분)으로 삼각형 만들기.
이때, [명제 20]에 따라
세 개의 선분 중 어느 두 선분의 길이를 합한 값은
항상 나머지 한 선분의 길이보다 길어야 한다.
사용되는 정의
- [정의 15] : 원은 하나의 특이한 선으로 둘러싸인 평면 도형이다. 이 특이한 선은 원의 둘레라고 부르며, 원의 중심으로부터 원의 둘레까지 뻗는 모든 직선들은 반지름이며, 그 길이는 모두 같다.
사용되는 공준
- [공준 1] : 두 점이 주어지면 두 점을 연결하는 직선을 그을 수 있다는 규칙
- [공준 3] : 임의의 한 점(A)과 임의의 간격(r)이 주어지면 해당 점(A)을 중심으로 하고, 일정한 간격(r)에 있는 점들로 원을 그릴 수 있다는 규칙
사용되는 명제
- [명제 3] : 길이가 같지 않은 주어진 두 종료된 직선(선분)에 대하여 길이가 긴 선분에서 짧은 선분과 같은 길이만큼 잘라내기
[명제 22]
세 개의 종료된 직선(선분)으로 삼각형 만들기.
이때, [명제 20]에 따라
세 개의 선분 중 어느 두 선분의 길이를 합한 값은
나머지 한 선분의 길이보다 길어야 한다.
※ 증명에 사용된 그림은 알지오매스 사이트를 통해 제작하였습니다.
- 0 -
세 개의 선분을 각각 A, B, C라고 하자.
이때 A+B > C, B+C > A, A+C > B를 만족한다.

- 1 -
어느 한 점 D를 시작점으로 하여 한 방향으로 무한히 연장하는
반직선 DE를 그린다.

- 2 -
[명제 3]에 따라, 점 D를 끝점으로 하고, 길이는 A와 같은 선분 DF를 그린다.

- 3 -
[명제 3]에 따라, 점 F를 끝점으로 하고, 길이는 B와 같은 선분 FG를 그린다.

- 4 -
[명제 3]에 따라, 점 G를 끝점으로 하고, 길이는 C와 같은 선분 GH를 그린다.

- 5 -
[공준 3]에 따라, 점 F를 중심으로 하고, 간격은 FD인 원 c₁을 그린다.

- 6 -
[공준 3]에 따라, 점 G를 중심으로 하고, 간격은 GH인 원 c₂를 그린다.

- 7 -
c₁ , c₂ 교점을 각각 K, L이라고 하자.

- 8 -
[공준 1]에 따라
점 F와 점 K를 연결하는 선분 KF, 그리고
점 K와 점 G를 연결하는 선분 KG를 그린다.
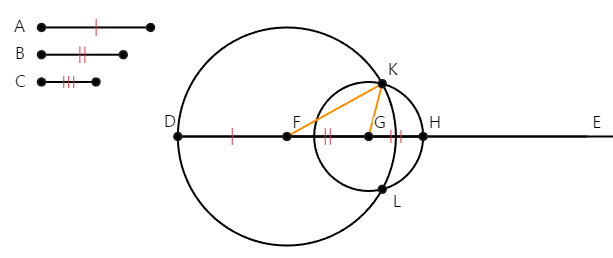
- 9 -
삼각형 △KFG에 대해서,
변 KF의 길이는 간격이 FD인 원 c₁의 반지름과 같다.
이때 FD = A와 같으므로 KF = A이다.
변 GK의 길이는 간격이 GH인 원 c₁의 반지름과 같다.
이때 GH = C와 같으므로 CK = C이다.
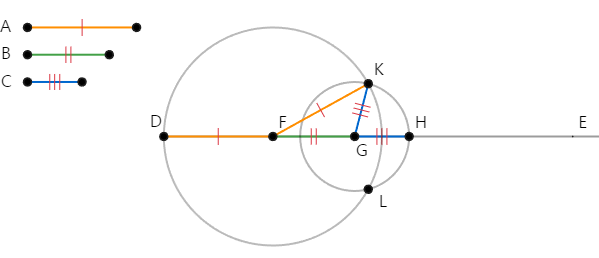
따라서 삼각형 △KFG의 세 변에 대해서, KF = A, FG = B, GK = C 이므로
주어진 세 개의 선분 중 어느 두 선분의 길이를 합한 값이
나머지 한 선분의 길이보다 길면
주어진 세 개의 선분으로 삼각형을 작도할 수 있다.
주관적 핵심
(주관적으로 느낀 핵심)
- 1 -
[명제 22]의 증명 과정의 핵심은
역 시 정의, 공리, 공준 그리고 이전에 증명된 명제들을 사용한다는 것이다.
- 2 -
이전 [명제 21]의 주관적 핵심 부분에서 언급하였듯이
명제 자체를 이해하는 데 있어서 어떤 것을 파악해야 하는지
탐구한 결과
명제 자체의 핵심은 다른 명제들과의 연관성을 파악하는 것이다.
즉,
명제가 다른 명제와 어떤 상호작용을 하는지 관계를 파악하는 것이다.
증명된 명제들이 어떤 명제에 사용되는지 파악함으로써,
증명된 명제 자체를 인식하는 것이다.
이는 [無에서 시작하는 수학]의 첫 번째 글이었던
“존재에 대해서”의 내용과 연결된다.
[수학][1] 숫자란 무엇인가, 그리고 존재란 무엇인가
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다. 숫자란 ‘수’를 표현하기 위한 ‘기호’이다 그렇다면 '수'는 무엇이고'기호'란 무엇인가'수'란 양(量), 개수, 온도
core-basic.tistory.com
해당 글에 따르면,
존재라는 것을 인식하고, 이해한다는 것은
다른 무언가 상호작용이 발생한다는 것이기에,
명제가 존재한다는 것을 인식하고, 이해한다는 것은
다른 명제와 상호작용이 발생하는 것과 같다.
따라서,
다른 명제와 어떤 상호작용이 이루어지는지 그 연관성을 파악할 수 있다면,
알고자 하는 명제를 이해하게 될 것이다.
따라서 명제들 사이의 관계도를 탐구해 보겠다.
이번 글은 요기서 마치며, 다음 주제는 이어서 1권 명제 23에 대해 탐구할 것 같다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 수학]' 카테고리의 다른 글
| [수학][28] 유클리드 기하학 <원론> 1권 - 중간 정리 (명제 1 ~ 명제 23) (0) | 2024.08.21 |
|---|---|
| [수학][27] 유클리드 기하학 <원론> 1권 - 24 (명제 23) (0) | 2024.08.20 |
| [수학][25] 유클리드 기하학 <원론> 1권 - 22 (명제 21) (0) | 2024.08.18 |
| [수학][24] 유클리드 기하학 <원론> 1권 - 21 (명제 20) (0) | 2024.08.17 |
| [수학][23] 유클리드 기하학 <원론> 1권 - 20 (명제 19) (0) | 2024.08.16 |