※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
이전 글을 통해서 유클리드 기하학 <원론> 1권 48개의 명제 중
명제 23에 대해 알아보았다.
이어서 명제 24에 대해 알아보겠다.
[수학][27] 유클리드 기하학 <원론> 1권 - 24 (명제 23)
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.이전 글을 통해서 유클리드 기하학 1권 48개의 명제 중명제 22에 대해 알아보았다.이어서 명제 23에 대해 알아보겠
core-basic.tistory.com
따라서 이번 글의 주제는
< 유클리드 기하학 <원론> 제1권 명제 24 >
두 삼각형에 대해서,
대응되는 두 변의 길이가 같으나 그 사잇각의 크기가 다를 때,
더 큰 사잇각을 가진 삼각형의 나머지 한 변의 길이가 더 길다.
사용되는 공준
- [공준 1] : 두 점이 주어지면 두 점을 연결하는 직선을 그을 수 있다는 기하학 규칙
사용되는 명제
- [명제 3] : 길이가 같지 않은 주어진 두 종료된 직선(선분)에 대하여 길이가 긴 선분에서 짧은 선분과 같은 길이만큼 잘라내기
- [명제 4] : 두 개의 삼각형이 존재할 때, 대응되는 두 변의 길이가 같고 그 사잇각의 크기가 같으면, 나머지 한 변과 두 각도 모두 같아지게 되면서, 두 삼각형은 합동이 된다. [SAS합동]
- [명제 5] : 이등변 삼각형은 두 밑각의 크기는 같고, 같은 두 변에 해당되는 직선이 연장하였을 때 밑각 아래에 있는 각들도 서로 같다.
- [명제 19] : 모든 삼각형에 대해서, 각이 더 큰 각일수록 마주 보는 대변의 길이도 더 길다.
- [명제 23] : 주어진 직선상의 한 점에서, 주어진 각과 같은 크기의 각도를 작도할 수 있다.
[명제 24]
두 삼각형에 대해서,
대응되는 두 변의 길이가 같으나 그 사잇각의 크기가 다를 때,
더 큰 사잇각을 가진 삼각형의 나머지 한 변의 길이가 더 길다.
※ 증명에 사용된 그림은 알지오매스 사이트를 통해 제작하였습니다.
- 0 -
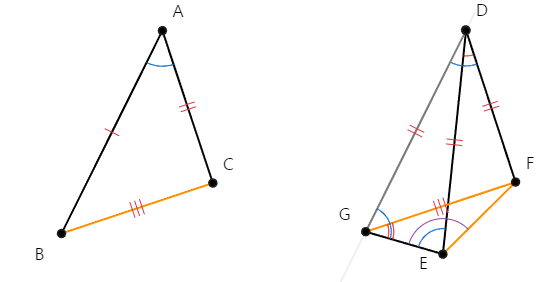
주어진 두 삼각형 △ABC, △DEF에 대해서
대응되는 두 변이 같고 ( AB = DE, AC = DF)
그 사잇각의 크기는 △ABC의 ∠BAC가 △DEF의 ∠EDF보다 더 크다고 하자.
( ∠BAC > ∠EDF )

<예상>
두 삼각형을 ‘비교’ 해야 하므로, 두 삼각형을 겹쳐놓아야 할 것이다.
또는 밑변을 ‘비교’ 해야 하므로, 두 밑변이 포함된 부등식을 유도할 것이다.
따라서
증명과정에서 위와 같은 상황을 유도하기 위해 어떠한 과정을 거치는지 살펴보자.
- 1 -
[명제 23]에 따라
△DEF의 점 D에서 ∠BAC와 같은 크기의 각 ∠FDG를 생성한다.
∠BAC = ∠GEF
(각을 생성한다는 것은 서로 다른 기울기를 가진 직선을 생성하는 것과 같다.)

<주관적 부분 핵심>
각이란 [정의 8]에 따르면, 두 직선이 만나 일직선이 되지 않을 때,
그 두 직선이 이루는 기울기이므로, 두 개의 직선이 있어야 각이 된다.
따라서
이미 주어진 하나의 직선이 있을 때,
각을 생성한다는 것은 특정 기울기를 가지는 직선을 하나 더 생성하는 것과 같다.
따라서
각을 생성한다는 것은 서로 다른 기울기를 가진 직선을 생성하는 것과 같다.
- 2 -
[명제 3]에 따라 △DEF의 점 D에서 ∠GDF를 생성을 생성했던 직선 위에
변 DE와 같은 길이를 가진 선분 DG를 생성한다.

< 주관적 부분 핵심 >
[명제 2]를 통해서, 원하는 점에서 주어진 선분들 중
원하는 길이와 같은 길이를 가진 선분을 생성할 수 있다.
[공준 3]에 따라
명제 2를 통해서 생성된 선분의 끝 점 중 하나를
원의 중심으로 하고, 선분의 길이를 간격으로 하는 원을 생성하면,
원의 중심으로부터 360° 모든 방향으로 생성된 선분과
같은 길이를 가진 선분을 추가로 생성할 수 있다.
그리고 이러한 과정이 [명제 3]이다.
- 3 -
[공준 1]에 따라,
점 G와 점 E를 그리고, 점 G와 점 F를 각각 연결하는 선분 GE와 GF를 생성한다.

- 4 -
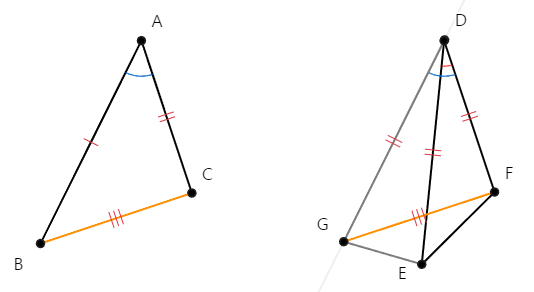
[명제 4]에 따라 △ABC, △DGF에 대해서
AB = DG, AC = DF, ∠BAC = ∠GDF 이므로 △ABC ≡ △DGF합동이다.
(SAS 합동)

- 5 -
따라서, 밑변 BC = GF이다.
- 6 -
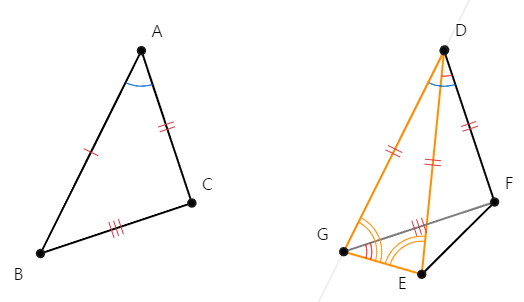
[명제 5]에 따라 △DGE에 대해서 DG = DE, 이등변 삼각형이므로
∠DGE = ∠DEG이다. 따라서 ∠DEG(=∠DGE) > ∠FGE이다.
- 7 -
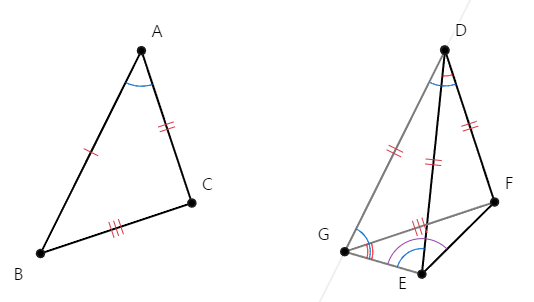
따라서 ∠FEG > ∠DEG(=∠DGE) > ∠FGE 또한, 성립한다.
- 8 -
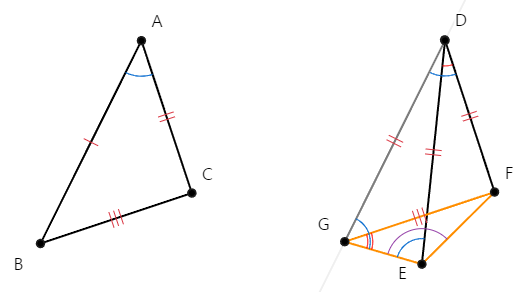
[명제 19]에 따라. △FEG에 대해서 ∠FEG > ∠FGE 이므로
∠FEG가 마주하는 변 FG 길이가 ∠FGE가 마주하는 변 FE 보다 더 길다.
( FG > FE )
- 9 -
이때 FG = BC 이므로 BC(=FG) > FE 가 성립한다.
BC는 △ABC의 밑변이고, FE는 △DEF의 밑변이다.
따라서 두 삼각형에 대해서,
대응되는 두 변의 길이가 같으나 그 사잇각의 크기가 다를 때,
더 큰 사잇각을 가진 삼각형의 나머지 한 변의 길이가 더 길다.
주관적 핵심
(주관적으로 느낀 핵심)
- 1 -
[명제 24]에 대한 핵심은 주관적 부분 핵심과 같다.
그리고, 이전부터 명제들 사이의 상호작용을
어떻게 파악해야 할지 탐구하였고, 그 결과
명제들을 크게 '비교'와 '생성' 두 분류로 나누었는데
이는 미흡한 점이 느껴졌다.
그런데 이번 [명제 24] 과정을 살펴보다가
새로운 분류가 떠오르게 되었다.
- 2 -
새로운 분류에 대해서,
우선 주관적 부분 핵심의 내용 일부를 가져오면,
이번 글 [명제 24]는 [명제 3]을 이용한다.
그런데 [명제 3]은 [명제 2]와 [공준 3]과 결합하여 증명된다.
이처럼 이전에 주관적 핵심에서도 언급하였듯이,
명제를 증명하는 데 있어서 정의, 공리, 공준뿐만 아니라, 명제도
사용한다는 것은 이미 알고 있다.
그런데 명제 1~명제 23을 크게 두 분류, 비교와 생성으로 분류하여
정리하는 글을 작성한 후 다시 보니
보이지 않았던 분류가 보이기 시작했다.
(1) 정의, 공리, 공준을 통해서만 증명되는 명제
(2) 정의, 공리, 공준 그리고 증명된 명제를 통해서 증명되는 명제
즉,
정의, 공리, 공준을 통해서만 증명되는 명제를
기본 명제 / 초기 명제로 지칭하여 분류하고,
정의, 공리, 공준 그리고 증명된 명제를 통해서 증명되는 명제를
유도된 명제 / 파생 명제로 지칭하여 분류할 수 있다는 것이다.
결국 중간 정리에서, 명제의 순서는 상관없다고 언급하였던 것은
실수였으며, 오히려 명제 순서는 명제들의 상호작용에 있어서 중요했다.
더 나아가
몇 개의 초기 명제들로 이루어졌는지에 따라 단계를 나눌 수도 있을 것 같다.
정의, 공리, 공준만을 사용하여 증명된 명제를 [0 단계] : 초기 명제라 지칭할 때
정의, 공리, 공준 개수는 상관없이,
초기 명제 1개 사용 : [1 단계]
초기 명제 2개 사용 : [2 단계]
초기 명제 3개 사용 : [3 단계]
...
위와 같이 표현하는 것이다.
그리고
파생 명제로부터 또 파생되는 명제가 있을 경우,
증명할 파생 명제가 아닌, 증명에 사용되는 파생 명제의 경우
초기 명제와 정의, 공리, 공준으로 쪼갤 수 있기 때문에
단계적 표현이 충분히 가능하다고 생각한다.
따라서 명제 정리 글에 대해 다시 한번 더 작성할 것 같다.
이번 글은 요기서 마치며, 다음 주제는 이어서 1권 명제 25에 대해 탐구할 것 같다.
※ 해당 게시글은 주제를 탐구하면서 주관적인 생각을 정리 한 글입니다.
'[無에서 시작하는 수학]' 카테고리의 다른 글
| [수학][28] 유클리드 기하학 <원론> 1권 - 중간 정리 (명제 1 ~ 명제 23) (0) | 2024.08.21 |
|---|---|
| [수학][27] 유클리드 기하학 <원론> 1권 - 24 (명제 23) (0) | 2024.08.20 |
| [수학][26] 유클리드 기하학 <원론> 1권 - 23 (명제 22) (0) | 2024.08.19 |
| [수학][25] 유클리드 기하학 <원론> 1권 - 22 (명제 21) (0) | 2024.08.18 |
| [수학][24] 유클리드 기하학 <원론> 1권 - 21 (명제 20) (0) | 2024.08.17 |